Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T01:36:58.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation forte pour les variétés avec une action d’un groupe linéaire

Part of: Arithmetic problems. Diophantine geometry Linear algebraic groups and related topics Arithmetic algebraic geometry

Published online by Cambridge University Press:  08 March 2018

Yang Cao
Yang Cao*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7, 53111 Bonn, Germany email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 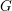$G$ be a connected linear algebraic group over a number field 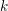$k$. Let 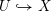$U{\hookrightarrow}X$ be a 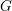$G$-equivariant open embedding of a 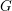$G$-homogeneous space 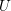$U$ with connected stabilizers into a smooth 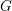$G$-variety 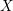$X$. We prove that 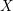$X$ satisfies strong approximation with Brauer–Manin condition off a set 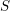$S$ of places of 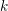$k$ under either of the following hypotheses:

  1. (i) 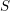$S$ is the set of archimedean places;

  2. (ii) 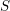$S$ is a non-empty finite set and 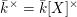$\bar{k}^{\times }=\bar{k}[X]^{\times }$.

The proof builds upon the case 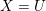$X=U$, which has been the object of several works.

Soit 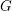$G$ un groupe linéaire connexe sur un corps de nombres 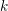$k$. Soit 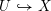$U{\hookrightarrow}X$ une inclusion 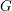$G$-équivariante d’un 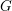$G$-espace homogène 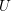$U$ à stabilisateurs connexes dans une 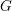$G$-variété lisse 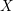$X$. On montre que 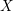$X$ satisfait l’approximation forte avec condition de Brauer–Manin hors d’un ensemble 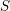$S$ de places de $k$ dans chacun des cas suivants :(i)

(i) 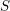$S$ est l’ensemble des places archimédiennes ;

(ii)

(ii) 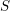$S$ est un ensemble fini non vide quelconque, et 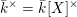$\bar{k}^{\times }=\bar{k}[X]^{\times }$.

La démonstration utilise le cas 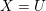$X=U$, qui a fait l’objet de divers travaux.

Keywords

approximation fortecohomologie étaleobstruction de Brauer–Maninespace homogène

MSC classification

Primary: 11G35: Varieties over global fields 14G05: Rational points 14G25: Global ground fields 20G35: Linear algebraic groups over adèles and other rings and schemes
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 4 , April 2018 , pp. 773 - 819
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).Google Scholar
Borovoi, M., The Brauer–Manin obstruction to the Hasse principle for homogeneous spaces with connected or abelian stabilizer , J. Reine Angew. Math. 473 (1996), 181–194.Google Scholar
Borovoi, M. and Demarche, C., Manin obstruction to strong approximation for homogeneous spaces , Comment. Math. Hev. 88 (2013), 1–54.CrossRefGoogle Scholar
Conrad, B., Weil and Grothendieck approaches to adelic points , Enseign. Math. 58 (2012), 61–97.Google Scholar
Cao, Y. and Xu, F., Strong approximation with Brauer–Manin obstruction for toric varieties, à paraître dans Ann. Inst. Fourier (Grenoble). Preprint (2013), arXiv:1311.7655.Google Scholar
Cao, Y. and Xu, F., Strong approximation with Brauer–Manin obstruction for groupic varieties, Preprint (2015), arXiv:1507.04340.Google Scholar
Cao, Y., Demarche, C. and Xu, F., Comparing descent obstruction and Brauer–Manin obstruction for open varieties, Preprint (2016), arXiv:1604.02709.Google Scholar
Colliot-Thélène, J.-L., Birational invariants, purity and the Gersten conjecture , in K-theory and algebraic geometry: connections with quadratic forms and division algebras, Proceedings of Symposia in Pure Mathematics, vol. 58, Part I, eds Jacob, W. and Rosenberg, A. (American Mathematical Society, Providence, RI, 1995), 1–64.Google Scholar
Colliot-Thélène, J.-L., Lectures on linear algebraic groups, notes, April 2007,http://www.math.u-psud.fr/∼colliot/BeijingLectures2Juin07.pdf.Google Scholar
Colliot-Thélène, J.-L., Résolutions flasques des groupes linéaires connexes , J. Reine Angew. Math. 618 (2008), 77–133.Google Scholar
Colliot-Thélène, J.-L. and Harari, D., Approximation forte en famille , J. Reine Angew. Math. 710 (2016), 173–198.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Principal homogeneous spaces under flasque tori, applications , J. Algebra 106 (1987), 148–205.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., La descente sur les variétés rationnelles, II , Duke Math. J. 54 (1987), 375–492.Google Scholar
Colliot-Thélène, J.-L. and Xu, F., Brauer–Manin obstruction for integral points of homogeneous spaces and representations by integral quadratic forms , Compositio Math. 145 (2009), 309–363.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Xu, F., Strong approximation for the total space of certain quadric fibrations , Acta Arith. 157 (2013), 169–199.Google Scholar
Demarche, C., Le défaut d’approximation forte dans les groupes linéaires connexes , Proc. Lond. Math. Soc. (3) 102 (2011), 563–597.CrossRefGoogle Scholar
Ekedahl, T., An effective version of Hilbert’s irreducibility theorem , in Séminaire de théorie des nombres de Paris, 1988–1989, Progress in Mathematics, vol. 91 (Birkhäuser, 1990), 241–248.Google Scholar
Grothendieck, A., Le groupe de Brauer, I, II, III , in Dix exposés sur la cohomologie des schémas (North-Holland & Masson, 1968).Google Scholar
Harari, D., Méthode des fibrations et obstruction de Manin , Duke Math. J. 75 (1994), 221–260.Google Scholar
Harari, D., Quelques propriétés d’approximation reliées à la cohomologie galoisienne d’un groupe algébrique fini , Bull. Soc. Math. France 135 (2007), 549–564.CrossRefGoogle Scholar
Harari, D., Le défaut d’approximation forte pour les groupes algébriques commutatifs , Algebra Number Theory 2 (2008), 595–611.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York–Heidelberg, 1977).CrossRefGoogle Scholar
Harari, D. and Szamuely, T., Arithmetic duality theorems for 1-motives , J. Reine Angew. Math. 578 (2005), 93–128.Google Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, 1980).Google Scholar
Platonov, V. P. and Rapinchuk, A. S., Algebraic groups and number theory, Pure and Applied Mathematics, vol. 139 (Academic, Boston, MA, 1994); translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Sansuc, J.-J., Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres , J. Reine Angew Math. 327 (1981), 12–80.Google Scholar
Serre, J.-P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5 (Springer, Berlin, 1965).CrossRefGoogle Scholar
Skorobogatov, A. N., On the fibration method for proving the Hasse principle and weak approximation , in Séminaire de théorie des nombres de Paris, 1988–1989, Progress in Mathematics, vol. 91 (Birkhäuser, Boston, MA, 1990), 205–219.Google Scholar
Skorobogatov, A. N., Torsors and rational points, Cambridge Tracts in Mathematics, vol. 144 (Cambridge University Press, Cambridge, 2001).CrossRefGoogle Scholar
Wei, D., Strong approximation for the variety containing a torus, Preprint (2014),arXiv:1403.1035.Google Scholar
Wei, D., Open descent and strong approximation, Preprint (2016), arXiv:1604.00610.Google Scholar