Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T01:06:44.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Annular Khovanov homology and knotted Schur–Weyl representations

Part of: Special aspects of infinite or finite groups Low-dimensional topology Groups and algebras in quantum theory

Published online by Cambridge University Press:  28 November 2017

J. Elisenda Grigsby ,
Anthony M. Licata  and
Stephan M. Wehrli
J. Elisenda Grigsby
Affiliation:
Boston College, Department of Mathematics, 5th floor Maloney, Chestnut Hill, MA 02467, USA email [email protected]
Anthony M. Licata
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, Australia email [email protected]
Stephan M. Wehrli
Affiliation:
Syracuse University, Department of Mathematics, 215 Carnegie, Syracuse, NY 13244, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

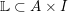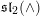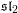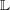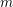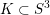Let $\mathbb{L}\subset A\times I$ be a link in a thickened annulus. We show that its sutured annular Khovanov homology carries an action of $\mathfrak{sl}_{2}(\wedge )$, the exterior current algebra of $\mathfrak{sl}_{2}$. When $\mathbb{L}$ is an $m$-framed $n$-cable of a knot $K\subset S^{3}$, its sutured annular Khovanov homology carries a commuting action of the symmetric group 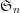$\mathfrak{S}_{n}$. One therefore obtains a ‘knotted’ Schur–Weyl representation that agrees with classical 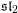$\mathfrak{sl}_{2}$ Schur–Weyl duality when 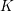$K$ is the Seifert-framed unknot.

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 81R50: Quantum groups and related algebraic methods 20F36: Braid groups; Artin groups
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 3 , March 2018 , pp. 459 - 502
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asaeda, M. M., Przytycki, J. H. and Sikora, A. S., Categorification of the Kauffman bracket skein module of I-bundles over surfaces , Algebr. Geom. Topol. 4 (2004), 1177–1210 (electronic).Google Scholar
Auroux, D., Grigsby, J. E. and Wehrli, S. M., Khovanov–Seidel quiver algebras and bordered Floer homology , Selecta Math. (N.S.) 20 (2014), 1–55.Google Scholar
Auroux, D., Grigsby, J. E. and Wehrli, S. M., Sutured Khovanov homology, Hochschild homology, and the Ozsváth–Szabó spectral sequence , Trans. Amer. Math. Soc. 367 (2015), 7103–7131.Google Scholar
Baldwin, J. A. and Grigsby, J. E., Categorified invariants and the braid group , Proc. Amer. Math. Soc. 143 (2015), 2801–2814.Google Scholar
Bar-Natan, D., Khovanov’s homology for tangles and cobordisms , Geom. Topol. 9 (2005), 1443–1499 (electronic).Google Scholar
Beliakova, A., Habiro, K., Lauda, A. D. and Živković, M., Trace decategorification of categorified quantum sl(2) , Math. Ann. 367 (2017), 397–440.Google Scholar
Beliakova, A., Putyra, K. and Wehrli, S. M., Quantum link homology via trace functor I, Preprint (2016), arXiv:1605.03523.Google Scholar
Bernstein, J., Trace in categories , in Operator algebras, unitary representations, enveloping algebras, and invariant theory (Paris, 1989), Progress in Mathematics, vol. 92 (Birkhäuser, Boston, MA, 1990), 417–423.Google Scholar
Brundan, J. and Stroppel, C., Highest weight categories arising from Khovanov’s diagram algebra I: cellularity , Mosc. Math. J. 11 (2011), 685–722.CrossRefGoogle Scholar
Carter, J. S., Kamada, S. and Saito, M., Surfaces in 4-space , in Low-dimensional topology, III, Encyclopaedia of Mathematical Sciences, vol. 142 (Springer, Berlin, 2004).Google Scholar
Carter, J. S. and Saito, M., Reidemeister moves for surface isotopies and their interpretation as moves to movies , J. Knot Theory Ramifications 2 (1993), 251–284.Google Scholar
Cautis, S. and Kamnitzer, J., Knot homology via derived categories of coherent sheaves. I. The sl(2)-case , Duke Math. J. 142 (2008), 511–588.CrossRefGoogle Scholar
Chen, Y. and Khovanov, M., An invariant of tangle cobordisms via subquotients of arc rings , Fund. Math. 225 (2014), 23–44.Google Scholar
Clark, D., Morrison, S. and Walker, K., Fixing the functoriality of Khovanov homology , Geom. Topol. 13 (2009), 1499–1582.Google Scholar
Greenstein, J. and Mazorchuk, V., Koszul duality for semidirect products and generalized Takiff algebras , Algebr. Represent. Theory 20 (2017), 675–694.Google Scholar
Grigsby, J. E. and Ni, Y., Sutured Khovanov homology distinguishes braids from other tangles , Math. Res. Lett. 21 (2014), 1263–1275.Google Scholar
Grigsby, J. E. and Wehrli, S. M., Khovanov homology, sutured Floer homology and annular links , Algebr. Geom. Topol. 10 (2010), 2009–2039.CrossRefGoogle Scholar
Grigsby, J. E. and Wehrli, S. M., On the colored Jones polynomial, sutured Floer homology, and knot Floer homology , Adv. Math. 223 (2010), 2114–2165.Google Scholar
Grigsby, J. E. and Wehrli, S. M., On gradings in Khovanov homology and sutured Floer homology , in Topology and geometry in dimension three, Contemporary Mathematics, vol. 560 (American Mathematical Society, Providence, RI, 2011), 111–128.Google Scholar
Hedden, M. and Ni, Y., Khovanov module and the detection of unlinks , Geom. Topol. 17 (2013), 3027–3076.Google Scholar
Huerfano, R. S. and Khovanov, M., A category for the adjoint representation , J. Algebra 246 (2001), 514–542.Google Scholar
Hunt, H., Keese, H., Licata, A. M. and Morrison, S., Computing annular Khovanov homology, Preprint (2015), arXiv:1505.04484.Google Scholar
Jacobsson, M., An invariant of link cobordisms from Khovanov homology , Algebr. Geom. Topol. 4 (2004), 1211–1251 (electronic).Google Scholar
Juhász, A., Holomorphic discs and sutured manifolds , Algebr. Geom. Topol. 6 (2006), 1429–1457 (electronic).Google Scholar
Khovanov, M., A categorification of the Jones polynomial , Duke Math. J. 101 (2000), 359–426.Google Scholar
Khovanov, M., Patterns in knot cohomology. I , Experiment. Math. 12 (2003), 365–374.Google Scholar
Khovanov, M., Categorifications of the colored Jones polynomial , J. Knot Theory Ramifications 14 (2005), 111–130.Google Scholar
Khovanov, M. and Rozansky, L., Matrix factorizations and link homology , Fund. Math. 199 (2008), 1–91.Google Scholar
Lauda, A. D., A categorification of quantum sl(2) , Adv. Math. 225 (2010), 3327–3424.Google Scholar
Lee, E. S., An endomorphism of the Khovanov invariant , Adv. Math. 197 (2005), 554–586.CrossRefGoogle Scholar
Loupias, M., Représentations indécomposables de dimension finie des algèbres de Lie , Manuscripta Math. 6 (1972), 365–379.CrossRefGoogle Scholar
Morrison, S. and Nieh, A., On Khovanov’s cobordism theory for su3 knot homology , J. Knot Theory Ramifications 17 (2008), 1121–1173.Google Scholar
Ozsváth, P. and Szabó, Z., On the Heegaard Floer homology of branched double-covers , Adv. Math. 194 (2005), 1–33.Google Scholar
Plamenevskaya, O., Transverse knots and Khovanov homology , Math. Res. Lett. 13 (2006), 571–586.Google Scholar
Przytycki, J. H. and Sikora, A. S., On skein algebras and Sl2(C)-character varieties , Topology 39 (2000), 115–148.CrossRefGoogle Scholar
Queffelec, H. and Rose, D. E. V., Sutured annular Khovanov–Rozansky homology, Trans. Amer. Math. Soc., to appear. Preprint (2015), arXiv:1506.08188.Google Scholar
Rasmussen, J., Khovanov’s invariant for closed surfaces, Preprint (2015),arXiv:math/0502527 [math.GT].Google Scholar
Rasmussen, J., Khovanov homology and the slice genus , Invent. Math. 182 (2010), 419–447.Google Scholar
Roberts, L. P., On knot Floer homology in double branched covers , Geom. Topol. 17 (2013), 413–467.Google Scholar
Seidel, P. and Smith, I., A link invariant from the symplectic geometry of nilpotent slices , Duke Math. J. 134 (2006), 453–514.Google Scholar
Stroppel, C., Categorification of the Temperley–Lieb category, tangles, and cobordisms via projective functors , Duke Math. J. 126 (2005), 547–596.CrossRefGoogle Scholar
Sussan, J., Category O and sl(k) link invariants, PhD thesis, Yale University, ProQuest LLC, Ann Arbor, MI (2007).Google Scholar
Tsilevich, N. and Vershik, A., On a relation between the basic representation of the affine Lie algebra $\text{sl}(2)$ and a Schur–Weyl representation of the infinite symmetric group, Preprint (2014), arXiv:1403.1558.Google Scholar
Webster, B., Tensor product algebras, Grassmannians and Khovanov homology , in Physics and mathematics of link homology, Contemporary Mathematics, vol. 680 (American Mathematical Society, Providence, RI, 2016), 23–58.CrossRefGoogle Scholar