Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kirsebom, Maxim
Kunde, Philipp
and
Persson, Tomas
2020.
Shrinking targets and eventually always hitting points for interval maps.
Nonlinearity,
Vol. 33,
Issue. 2,
p.
892.
Beresnevich, Victor
and
Velani, Sanju
2020.
Number Theory Meets Wireless Communications.
p.
1.
Huang, Lingling
Wu, Jun
and
Xu, Jian
2020.
Metric properties of the product of consecutive partial quotients in continued fractions.
Israel Journal of Mathematics,
Vol. 238,
Issue. 2,
p.
901.
Ganotaki, Charis
and
Persson, Tomas
2021.
On eventually always hitting points.
Monatshefte für Mathematik,
Vol. 196,
Issue. 4,
p.
763.
Kleinbock, Dmitry
and
Skenderi, Mishel
2021.
Khintchine-type theorems for values of subhomogeneous functions at integer points.
Monatshefte für Mathematik,
Vol. 194,
Issue. 3,
p.
523.
Wang, Bao-Wei
and
Zhang, Guo-Hua
2021.
A dynamical dimension transference principle for dynamical diophantine approximation.
Mathematische Zeitschrift,
Vol. 298,
Issue. 1-2,
p.
161.
Kim, Taehyeong
and
Kim, Wooyeon
2022.
Hausdorff measure of sets of Dirichlet non-improvable affine forms.
Advances in Mathematics,
Vol. 403,
Issue. ,
p.
108353.
BAKHTAWAR, AYREENA
2022.
HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET.
Journal of the Australian Mathematical Society,
Vol. 112,
Issue. 1,
p.
1.
Kleinbock, Dmitry
Strömbergsson, Andreas
and
Yu, Shucheng
2022.
A measure estimate in geometry of numbers and improvements to Dirichlet's theorem.
Proceedings of the London Mathematical Society,
Vol. 125,
Issue. 4,
p.
778.
Bos, Philip
Hussain, Mumtaz
and
Simmons, David
2023.
The generalised Hausdorff measure of sets of Dirichlet non-improvable numbers.
Proceedings of the American Mathematical Society,
Bakhtawar, Ayreena
and
Simmons, David
2023.
Generalised Hausdorff measure of sets of Dirichlet non-improvable matrices in higher dimensions.
Research in Number Theory,
Vol. 9,
Issue. 3,
LI, BIXUAN
WANG, BAOWEI
and
XU, JIAN
2023.
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 8,
p.
2707.
Holland, Mark
Kirsebom, Maxim
Kunde, Philipp
and
Persson, Tomas
2024.
Dichotomy results for eventually always hitting time statistics and almost sure growth of extremes.
Transactions of the American Mathematical Society,
WANG, BO
and
LI, BING
2024.
METRIC RESULTS FOR THE EVENTUALLY ALWAYS HITTING POINTS AND LEVEL SETS IN SUBSHIFT WITH SPECIFICATION.
Fractals,
Vol. 32,
Issue. 06,
Datta, Shreyasi
and
Xu, Yewei
2025.
Singular Vectors and ψ-Dirichlet Numbers over Function Field.
Journal de théorie des nombres de Bordeaux,
Vol. 36,
Issue. 3,
p.
1021.
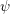 $\unicode[STIX]{x1D713}$ guaranteeing that for almost all (or almost no) pairs
$\unicode[STIX]{x1D713}$ guaranteeing that for almost all (or almost no) pairs 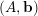 $(A,\mathbf{b})$, where
$(A,\mathbf{b})$, where 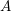 $A$ is a real
$A$ is a real 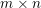 $m\times n$ matrix and
$m\times n$ matrix and 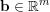 $\mathbf{b}\in \mathbb{R}^{m}$, the system
$\mathbf{b}\in \mathbb{R}^{m}$, the system 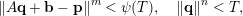 $$\begin{eqnarray}\Vert A\mathbf{q}+\mathbf{b}-\mathbf{p}\Vert ^{m}<\unicode[STIX]{x1D713}(T),\quad \Vert \mathbf{q}\Vert ^{n}<T,\end{eqnarray}$$
$$\begin{eqnarray}\Vert A\mathbf{q}+\mathbf{b}-\mathbf{p}\Vert ^{m}<\unicode[STIX]{x1D713}(T),\quad \Vert \mathbf{q}\Vert ^{n}<T,\end{eqnarray}$$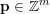 $\mathbf{p}\in \mathbb{Z}^{m}$,
$\mathbf{p}\in \mathbb{Z}^{m}$, 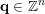 $\mathbf{q}\in \mathbb{Z}^{n}$ for all sufficiently large
$\mathbf{q}\in \mathbb{Z}^{n}$ for all sufficiently large 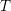 $T$. The proof consists of a reduction to a shrinking target problem on the space of grids in
$T$. The proof consists of a reduction to a shrinking target problem on the space of grids in 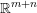 $\mathbb{R}^{m+n}$. We also comment on the homogeneous counterpart to this problem, whose
$\mathbb{R}^{m+n}$. We also comment on the homogeneous counterpart to this problem, whose 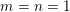 $m=n=1$ case was recently solved, but whose general case remains open.
$m=n=1$ case was recently solved, but whose general case remains open.