Published online by Cambridge University Press: 04 July 2019
In this paper we study the subgroup of the Picard group of Voevodsky’s category of geometric motives 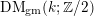 $\operatorname{DM}_{\text{gm}}(k;\mathbb{Z}/2)$ generated by the reduced motives of affine quadrics. Our main tools here are the functors of Bachmann [On the invertibility of motives of affine quadrics, Doc. Math. 22 (2017), 363–395], but we also provide an alternative method. We show that the group in question can be described in terms of indecomposable direct summands in the motives of projective quadrics over
$\operatorname{DM}_{\text{gm}}(k;\mathbb{Z}/2)$ generated by the reduced motives of affine quadrics. Our main tools here are the functors of Bachmann [On the invertibility of motives of affine quadrics, Doc. Math. 22 (2017), 363–395], but we also provide an alternative method. We show that the group in question can be described in terms of indecomposable direct summands in the motives of projective quadrics over 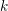 $k$. In particular, we describe all the relations among the reduced motives of affine quadrics. We also extend the criterion of motivic equivalence of projective quadrics.
$k$. In particular, we describe all the relations among the reduced motives of affine quadrics. We also extend the criterion of motivic equivalence of projective quadrics.