Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T01:52:24.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Vanishing and comparison theorems in rigid analytic geometry

Part of: (Co)homology theory Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  26 December 2019

David Hansen
David Hansen*
Affiliation:
Max Planck Institute for Mathematics, Vivatsgasse 7,Bonn53111, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a rigid analytic analogue of the Artin–Grothendieck vanishing theorem. Precisely, we prove (under mild hypotheses) that the geometric étale cohomology of any Zariski-constructible sheaf on any affinoid rigid space 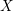$X$ vanishes in all degrees above the dimension of 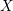$X$. Along the way, we show that branched covers of normal rigid spaces can often be extended across closed analytic subsets, in analogy with a classical result for complex analytic spaces. We also prove some new comparison theorems relating the étale cohomology of schemes and rigid analytic varieties, and give some applications of them. In particular, we prove a structure theorem for Zariski-constructible sheaves on characteristic-zero affinoid spaces.

Keywords

rigid analytic spacesétale cohomologyArtin–Grothendieck vanishingcomparison theorems

MSC classification

Primary: 14G22: Rigid analytic geometry 14F05: Sheaves, derived categories of sheaves and related constructions 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 2 , February 2020 , pp. 299 - 324
Copyright
© The Author 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreotti, A. and Frankel, T., The Lefschetz theorem on hyperplane sections, Ann. of Math. (2) 69 (1959), 713–717; MR 0177422.CrossRefGoogle Scholar
Bartenwerfer, W., Der erste Riemannsche Hebbarkeitssatz im nichtarchimedischen Fall, J. reine angew. Math. 286–287 (1976), 144–163; MR 0422680.Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161; MR 1259429.CrossRefGoogle Scholar
Berkovich, V. G., Vanishing cycles for formal schemes, Invent. Math. 115 (1994), 539–571; MR 1262943.CrossRefGoogle Scholar
Berkovich, V. G., Vanishing cycles for formal schemes. II, Invent. Math. 125 (1996), 367–390; MR 1395723.CrossRefGoogle Scholar
Berkovich, V. G., Finiteness theorems for vanishing cycles of formal schemes, Israel J. Math. 210 (2015), 147–191; MR 3430272.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis: a systematic approach to rigid analytic geometry, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984); MR 746961.CrossRefGoogle Scholar
Conrad, B., Irreducible components of rigid spaces, Ann. Inst. Fourier (Grenoble) 49 (1999), 473–541; MR 1697371.CrossRefGoogle Scholar
Dethloff, G. and Grauert, H., Seminormal complex spaces, in Several complex variables, VII, Encyclopaedia of Mathematical Sciences, vol. 74 (Springer, Berlin, 1994), 183–220;MR 1326621.CrossRefGoogle Scholar
Elkik, R., Solutions d’équations à coefficients dans un anneau hensélien, Ann. Sci. Éc. Norm. Supér. (4) 6 (1974), 553–603; MR 0345966.CrossRefGoogle Scholar
Greco, S., Two theorems on excellent rings, Nagoya Math. J. 60 (1976), 139–149; MR 0409452.CrossRefGoogle Scholar
Hansen, D., A primer on reflexive sheaves, Appendix to the preprint ‘On the Kottwitz conjecture for local Shimura varieties’ by Tasho Kaletha and Jared Weinstein. Preprint (2017),arXiv:1709.06651 [math.NT].Google Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30 (Vieweg, Braunschweig, 1996); MR 1734903.CrossRefGoogle Scholar
Illusie, L., Laszlo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, Astérisque 363–364 (2014).Google Scholar
Kiehl, R., Der Endlichkeitssatz für eigentliche Abbildungen in der nichtarchimedischen Funktionentheorie, Invent. Math. 2 (1967), 191–214; MR 0210948.CrossRefGoogle Scholar
Kiehl, R., Die de Rham Kohomologie algebraischer Mannigfaltigkeiten über einem bewerteten Körper, Publ. Math. Inst. Hautes Études Sci. 33 (1967), 5–20; MR 0229644.Google Scholar
Lütkebohmert, W., Riemann’s existence problem for a p-adic field, Invent. Math. 111 (1993), 309–330; MR 1198812.CrossRefGoogle Scholar
Mitsui, K., Criterion for minimality of rigid analytic surfaces, Preprint, https://www.math.kyoto-u.ac.jp/preprint/2009/20mitsui.pdf.Google Scholar
Nori, M. V., Constructible sheaves, Algebra, arithmetic and geometry, Parts I, II (Mumbai, 2000), Tata Institute of Fundamental Research Studies in Mathematics, vol. 16, 471–491 (Tata Institute of Fundamental Research, Bombay, 2002); MR 1940678.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L. (eds), Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 – Théorie des topos et cohomologie étale des schémas (SGA 4), Tome 3, Lecture Notes in Mathematics, vol. 305 (Springer, Berlin–New York, 1973), avec la collaboration de P. Deligne et B. Saint-Donat; MR 0354654.Google Scholar
The Stacks Project Authors, Stacks project (2017), http://stacks.math.columbia.edu.Google Scholar
Temkin, M., Functorial desingularization over Q : boundaries and the embedded case, Israel J. Math. 224 (2018), 455–504; MR 3799764.CrossRefGoogle Scholar
Valabrega, P., On the excellent property for power series rings over polynomial rings, J. Math. Kyoto Univ. 15 (1975), 387–395; MR 0376677.CrossRefGoogle Scholar
Valabrega, P., A few theorems on completion of excellent rings, Nagoya Math. J. 61 (1976), 127–133; MR 0407007.CrossRefGoogle Scholar