Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T16:49:07.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Towards an explicit local Jacquet–Langlands correspondence beyond the cuspidal case

Part of: Lie groups

Published online by Cambridge University Press:  27 August 2019

Vincent Sécherre  and
Shaun Stevens
Vincent Sécherre
Affiliation:
Laboratoire de Mathématiques de Versailles, UVSQ, CNRS, Université Paris-Saclay, 78035 Versailles, France email [email protected]
Shaun Stevens
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show how the modular representation theory of inner forms of general linear groups over a non-Archimedean local field can be brought to bear on the complex theory in a remarkable way. Let 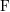$\text{F}$ be a non-Archimedean locally compact field of residue characteristic 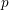$p$, and let 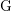$\text{G}$ be an inner form of the general linear group 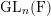$\text{GL}_{n}(\text{F})$ for 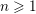$n\geqslant 1$. We consider the problem of describing explicitly the local Jacquet–Langlands correspondence 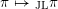$\unicode[STIX]{x1D70B}\mapsto _{\text{JL}}\unicode[STIX]{x1D70B}$ between the complex discrete series representations of 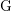$\text{G}$ and 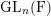$\text{GL}_{n}(\text{F})$, in terms of type theory. We show that the congruence properties of the local Jacquet–Langlands correspondence exhibited by A. Mínguez and the first author give information about the explicit description of this correspondence. We prove that the problem of the invariance of the endo-class by the Jacquet–Langlands correspondence can be reduced to the case where the representations $\unicode[STIX]{x1D70B}$ and 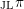$_{\text{JL}}\unicode[STIX]{x1D70B}$ are both cuspidal with torsion number 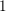$1$. We also give an explicit description of the Jacquet–Langlands correspondence for all essentially tame discrete series representations of 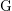$\text{G}$, up to an unramified twist, in terms of admissible pairs, generalizing previous results by Bushnell and Henniart. In positive depth, our results are the first beyond the case where $\unicode[STIX]{x1D70B}$ and 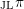$_{\text{JL}}\unicode[STIX]{x1D70B}$ are both cuspidal.

Keywords

Jacquet–Langlands correspondenceℓ-blockscongruences mod ℓendo-classadmissible pairrectifier

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 10 , October 2019 , pp. 1853 - 1887
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badulescu, A. I., Correspondance de Jacquet–Langlands en caractéristique non nulle , Ann. Sci. Éc. Norm. Supér. (4) 35 (2002), 695–747.Google Scholar
Badulescu, A. I., Jacquet–Langlands et unitarisabilité , J. Inst. Math. Jussieu 6 (2007), 349–379.Google Scholar
Broussous, P., Extension du formalisme de Bushnell et Kutzko au cas d’une algèbre à division , Proc. Lond. Math. Soc. (3) 77 (1998), 292–326.Google Scholar
Broussous, P., Transfert du pseudo-coefficient de Kottwitz et formules de caractère pour la série discrète de GL(N) sur un corps local , Canad. J. Math. 66 (2014), 241–283.Google Scholar
Broussous, P. and Schneider, P., Type theory and coefficient systems on the building , Bull. Soc. Math. France 145 (2017), 97–159.Google Scholar
Broussous, P., Sécherre, V. and Stevens, S., Smooth representations of GLm(D), V: endo-classes , Doc. Math. 17 (2012), 23–77.Google Scholar
Bushnell, C. J. and Henniart, G., Correspondance de Jacquet–Langlands explicite II: le cas de degré égal à la caractéristique résiduelle , Manuscripta Math. 102 (2000), 211–225.Google Scholar
Bushnell, C. J. and Henniart, G., Local tame lifting for GL(N), I: simple characters , Publ. Math. Inst. Hautes Études Sci. 83 (1996), 105–233.Google Scholar
Bushnell, C. J. and Henniart, G., Local tame lifting for GL(N), IV: simple characters and base change , J. Lond. Math. Soc. 87 (2003), 337–362.Google Scholar
Bushnell, C. J. and Henniart, G., Local tame lifting for GL(N), III: explicit base change and Jacquet–Langlands correspondence , J. Reine Angew. Math. 580 (2005a), 39–100.Google Scholar
Bushnell, C. J. and Henniart, G., The essentially tame local Langlands correspondence, I , J. Amer. Math. Soc. 18 (2005b), 685–710.Google Scholar
Bushnell, C. J. and Henniart, G., The essentially tame local Langlands correspondence, III: the general case , Proc. Lond. Math. Soc. (3) 101 (2010), 497–553.Google Scholar
Bushnell, C. J. and Henniart, G., The essentially tame Jacquet–Langlands correspondence for inner forms of GL(n) , Pure Appl. Math. Q. 7 (2011a), 469–538.Google Scholar
Bushnell, C. J. and Henniart, G., Explicit functorial correspondences for level 0 representations of p-adic linear groups , J. Number Theory 131 (2011b), 309–331.Google Scholar
Bushnell, C. J. and Henniart, G., To an effective local Langlands correspondence , Mem. Amer. Math. Soc. 231 (2014), 1–88.Google Scholar
Bushnell, C. J. and Kutzko, P. C., The admissible dual of GL(N) via compact open subgroups (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Dat, J.-F., Un cas simple de correspondance de Jacquet–Langlands modulo ℓ , Proc. Lond. Math. Soc. 104 (2012), 690–727.Google Scholar
Deligne, P., Kazhdan, D. and Vignéras, M.-F., Représentations des algèbres centrales simples p-adiques , in Representations of reductive groups over a local field (Hermann, Paris, 1984), 33–117.Google Scholar
Dipper, R., On the decomposition numbers of the finite general linear groups. II , Trans. Amer. Math. Soc. 292 (1985), 123–133.Google Scholar
Dotto, A., The inertial Jacquet–Langlands correspondence, Preprint (2017), arXiv:1707.00635.Google Scholar
Green, J. A., The characters of the finite general linear groups , J. Algebra 184 (1996), 839–851.Google Scholar
Helm, D., The Bernstein center of the category of smooth W(k)[GLn(F)]-modules , Forum Math. Sigma 4 (2016), e11.Google Scholar
Henniart, G., Correspondance de Jacquet–Langlands explicite I: le cas modéré de degré premier , in Séminaire de théorie des nombres de Paris 1990-91, Progress in Mathematics, vol. 38 (Birkhäuser, Boston, MA, 1993).Google Scholar
Howe, R. E., Tamely ramified supercuspidal representations of GLn , Pacific J. Math. 73 (1977), 437–460.Google Scholar
Imai, N. and Tsushima, T., Local Jacquet–Langlands correspondences for simple supercuspidal representations , Kyoto J. Math. 58 (2018), 623–638.Google Scholar
Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Lecture Notes in Mathematics, vol. 114 (Springer, Berlin, 1970).Google Scholar
Mínguez, A. and Sécherre, V., Représentations lisses modulo ℓ de GLm(D) , Duke Math. J. 163 (2014), 795–887.Google Scholar
Mínguez, A. and Sécherre, V., Types modulo ℓ pour les formes intérieures de GLn sur un corps local non archimédien, avec un appendice par V. Sécherre et S. Stevens , Proc. Lond. Math. Soc. 109 (2014), 823–891.Google Scholar
Mínguez, A. and Sécherre, V., Représentations modulaires de GLn(q) en caractéristique non naturelle , in Trends in number theory, Contemporary Mathematics, vol. 649 (American Mathematical Society, Providence, RI, 2015), 163–183.Google Scholar
Mínguez, A. and Sécherre, V., Correspondance de Jacquet–Langlands locale et congruences modulo ℓ , Invent. Math. 208 (2017), 553–631.Google Scholar
Rogawski, J., Representations of GL(n) and division algebras over a p-adic field , Duke Math. J. 50 (1983), 161–196.Google Scholar
Sécherre, V., Représentations lisses de GLm(D), I: caractères simples , Bull. Soc. Math. France 132 (2004), 327–396.Google Scholar
Sécherre, V., Représentations lisses de GLm(D), II: 𝛽-extensions , Compos. Math. 141 (2005), 1531–1550.Google Scholar
Sécherre, V., Représentations lisses de GLm(D), III: types simples , Ann. Sci. Éc. Norm. Supér. 38 (2005), 951–977.Google Scholar
Sécherre, V. and Stevens, S., Représentations lisses de GLm(D), IV: représentations supercuspidales , J. Inst. Math. Jussieu 7 (2008), 527–574.Google Scholar
Sécherre, V. and Stevens, S., Smooth representations of GLm(D), VI: semisimple types , Int. Math. Res. Not. 13 (2012), 2994–3039.Google Scholar
Sécherre, V. and Stevens, S., Block decomposition of the category of ℓ-modular smooth representations of GLn(F) and its inner forms , Ann. Sci. Éc. Norm. Supér. 49 (2016), 669–709.Google Scholar
Silberger, A. J. and Zink, E.-W., The characters of the generalized Steinberg representations of finite general linear groups on the regular elliptic set , Trans. Amer. Math. Soc. 352 (2000), 3339–3356.Google Scholar
Silberger, A. J. and Zink, E.-W., Weak explicit matching for level zero discrete series of unit groups of 𝔭-adic simple algebras , Canad. J. Math. 55 (2003), 353–378.Google Scholar
Silberger, A. J. and Zink, E.-W., An explicit matching theorem for level zero discrete series of unit groups of 𝔭-adic simple algebras , J. Reine Angew. Math. 585 (2005), 173–235.Google Scholar
Tadić, M., Induced representations of GL(n, A) for p-adic division algebras A , J. Reine Angew. Math. 405 (1990), 48–77.Google Scholar
Vignéras, M.-F., Représentations l-modulaires d’un groupe réductif p-adique avec l≠p , Progress in Mathematics, vol 137 (Birkhäuser, Boston, MA, 1996).Google Scholar
Vignéras, M.-F., On highest Whittaker models and integral structures , in Contributions to automorphic forms, geometry and number theory: Shalikafest 2002 (Johns Hopkins University Press, Baltimore, MD, 2004), 773–801.Google Scholar
Zelevinski, A., Induced representations of reductive 𝔭-adic groups. II. On irreducible representations of GL(n) , Ann. Sci. Éc. Norm. Supér. (4) 13 (1980), 165–210.Google Scholar
Zsigmondy, K., Zur Theorie der Potenzreste , Monatsh. Math. 3 (1892), 265–284.Google Scholar