Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T12:25:06.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Theta functions, fourth moments of eigenforms, and the sup-norm problem I

Part of: Discontinuous groups and automorphic forms Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  03 April 2025

Ilya Khayutin  and
Raphael S. Steiner Open the ORCID record for Raphael S. Steiner [Opens in a new window]
Ilya Khayutin
Affiliation:
Department of Mathematics, Northwestern University, Evanston IL 60203, USA
Raphael S. Steiner
Affiliation:
Computing Systems Lab, Huawei Zurich Research Center, Thurgauerstrasse 80, CH-8050 Zurich, Switzerland [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give sharp point-wise bounds in the weight-aspect on fourth moments of modular forms on arithmetic hyperbolic surfaces associated to Eichler orders. Thereby, we strengthen a result of Xia and extend it to co-compact lattices. We realize this fourth moment by constructing a holomorphic theta kernel on 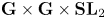$\mathbf {G} \times \mathbf {G} \times \mathbf {SL}_{2}$, for 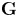$\mathbf {G}$ an indefinite inner form of 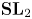$\mathbf {SL}_2$ over 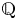$\mathbb {Q}$, based on the Bergman kernel, and considering its 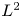$L^2$-norm in the Weil variable. The constructed theta kernel further gives rise to new elementary theta series for integral quadratic forms of signature 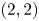$(2,2)$.

Keywords

sup-normholomorphic formstheta functiontheta correspondencefourth moment

MSC classification

Primary: 11F72: Spectral theory; Selberg trace formula
Secondary: 11F11: Holomorphic modular forms of integral weight 11F27: Theta series; Weil representation; theta correspondences 11F70: Representation-theoretic methods; automorphic representations over local and global fields 58J50: Spectral problems; spectral geometry; scattering theory
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 12 , December 2024 , pp. 2916 - 2969
Check for updates
Copyright
© The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Atkin, A. O. L. and Lehner, J., Hecke operators on $\Gamma _{0}(m)$, Math. Ann. 185 (1970), 134–160.Google Scholar
Assing, E., On sup-norm bounds part I: ramified Maaß newforms over number fields, J. Eur. Math. Soc. (JEMS) 26 (2024), 1559–1609.Google Scholar
Blomer, V. and Holowinsky, R., Bounding sup-norms of cusp forms of large level, Invent. Math. 179 (2010), 645–681.CrossRefGoogle Scholar
Blomer, V., Harcos, G. and Milićević, D., Bounds for eigenforms on arithmetic hyperbolic 3-manifolds, Duke Math. J. 165 (2016), 625–659.CrossRefGoogle Scholar
Blomer, V., Harcos, G., Maga, P. and Milićević, D., The sup-norm problem for GL(2) over number fields, J. Eur. Math. Soc. (JEMS) 22 (2020), 1–53.Google Scholar
Blomer, V., Khan, R. and Young, M., Distribution of mass of holomorphic cusp forms, Duke Math. J. 162 (2013), 2609–2644.Google Scholar
Blomer, V. and Michel, P., Sup-norms of eigenfunctions on arithmetic ellipsoids, Int. Math. Res. Not. IMRN 2011 (2011), 4934–4966.Google Scholar
Blomer, V. and Michel, P., Hybrid bounds for automorphic forms on ellipsoids over number fields, J. Inst. Math. Jussieu 12 (2013), 727–758.Google Scholar
Blomer, V. and Maga, P., The sup-norm problem for PGL(4), Int. Math. Res. Not. IMRN 2015 (2015), 5311–5332.CrossRefGoogle Scholar
Blomer, V. and Maga, P., Subconvexity for sup-norms of cusp forms on ${\rm {PGL}}(n)$, Selecta Math. (N.S.) 22 (2016), 1269–1287.Google Scholar
Borel, A., Some finiteness properties of adele groups over number fields, Publ. Math. Inst. Hautes Études Sci. 16 (1963), 5–30.Google Scholar
Blomer, V. and Pohl, A., The sup-norm problem on the Siegel modular space of rank two, Amer. J. Math. 138 (2016), 999–1027.Google Scholar
Chinburg, T. and Friedman, E., An embedding theorem for quaternion algebras, J. Lond. Math. Soc. (2) 60 (1999), 33–44.Google Scholar
Chu, M. and Li, H., Small generators of cocompact arithmetic Fuchsian groups, Proc. Amer. Math. Soc. 144 (2016), 5121–5127.Google Scholar
Das, S. and Sengupta, J., $L^{\infty }$ norms of holomorphic modular forms in the case of compact quotient, Forum Math. 27 (2015), 1987–2001.CrossRefGoogle Scholar
Das, S. and Sengupta, J., $L^\infty$ norms of holomorphic modular forms in the case of compact quotient, Preprint (2020), arXiv:1301.3677v3.Google Scholar
Gross, B. H. and Zagier, D. B., Heegner points and derivatives of $L$-series, Invent. Math. 84 (1986), 225–320.CrossRefGoogle Scholar
Hoffstein, J. and Lockhart, P., Coefficients of Maass forms and the Siegel zero, Ann. of Math. (2) 140 (1994), 161–181; with an appendix by D. Goldfeld, J. Hoffstein and D. Lieman.CrossRefGoogle Scholar
Hu, Y., Nelson, P. D. and Saha, A., Some analytic aspects of automorphic forms on ${\rm {GL}}(2)$ of minimal type, Comment. Math. Helv. 94 (2019), 767–801.Google Scholar
Hu, Y. and Saha, A., Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity, Compos. Math. 156 (2020), 2368–2398.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level: II, Int. Math. Res. Not. IMRN 2012 (2012), 4764–4774.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. III, Math. Ann. 356 (2013), 209–216.CrossRefGoogle Scholar
Ichino, A., Trilinear forms and the central values of triple product $L$-functions, Duke Math. J. 145 (2008), 281–307.Google Scholar
Iwaniec, H. and Sarnak, P., $L^{\infty }$ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. (2) 141 (1995), 301–320.CrossRefGoogle Scholar
Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Lecture Notes in Mathematics, vol. 114 (Springer, Berlin–New York, 1970).CrossRefGoogle Scholar
Khan, R., On the fourth moment of holomorphic Hecke cusp forms, Ramanujan J. 34 (2014), 83–107.CrossRefGoogle Scholar
Kıral, E. M., Bounds on sup-norms of half-integral weight modular forms, Acta Arith. 165 (2014), 385–399.CrossRefGoogle Scholar
Khayutin, I., Nelson, P. D. and Steiner, R. S., Theta functions, fourth moments of eigenforms, and the sup-norm problem II, Forum Math. Pi 12 (2024), e11.Google Scholar
Marshall, S., Upper bounds for Maass forms on semisimple groups, Preprint (2014), arXiv:1405.7033.Google Scholar
Nelson, P. D., Equidistribution of cusp forms in the level aspect, Duke Math. J. 160 (2011), 467–501.CrossRefGoogle Scholar
Nelson, P. D., Evaluating modular forms on Shimura curves, Math. Comp. 84 (2015), 2471–2503.CrossRefGoogle Scholar
Nelson, P. D., Quantum variance on quaternion algebras, I, Preprint (2016), arXiv:1601.02526.Google Scholar
Nelson, P. D., Quantum variance on quaternion algebras, II, Preprint (2017), arXiv:1702.02669.Google Scholar
Nelson, P. D., Quantum variance on quaternion algebras, III, Preprint (2019), arXiv:1903.08686.Google Scholar
Nelson, P. D., Bounds for twisted symmetric square $L$-functions via half-integral weight periods, Forum Math. Sigma 8 (2020), e44.CrossRefGoogle Scholar
Petersson, H., Über eine Metrisierung der automorphen Formen und die Theorie der Poincaréschen Reihen, Math. Ann. 117 (1940), 453–537.CrossRefGoogle Scholar
Petersson, H., Einheitliche Begründung der Vollständigkeitssätze für die Poincaréschen Reihen von reeller Dimension bei beliebigen Grenzkreisgruppen von erster Art, Abh. Math. Semin. Hansischen Univ. 14 (1941), 22–60.Google Scholar
Ramacher, P. and Wakatsuki, S., Subconvex bounds for Hecke-Maass forms on compact arithmetic quotients of semisimple Lie groups, Math. Z. 298 (2021), 1383–1424.CrossRefGoogle Scholar
Saha, A., Hybrid sup-norm bounds for Maass newforms of powerful level, Algebra Number Theory 11 (2017), 1009–1045.CrossRefGoogle Scholar
Saha, A., On sup-norms of cusp forms of powerful level, J. Eur. Math. Soc. (JEMS) 19 (2017), 3549–3573.Google Scholar
Saha, A., Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, Math. Ann. 376 (2020), 609–644.CrossRefGoogle Scholar
Sarnak, P., Spectra of hyperbolic surfaces, Bull. Amer. Math. Soc. (N.S.) 40 (2003), 441–478.CrossRefGoogle Scholar
Selberg, A., On the zeros of Riemann's zeta-function, Skr. Norske Vid.-Akad. Oslo I 1942 (1942), 59.Google Scholar
Selberg, A., Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series, J. Indian Math. Soc. (N.S.) 20 (1956), 47–87.Google Scholar
Shimizu, H., Theta series and automorphic forms on ${\rm GL}_{2}$, J. Math. Soc. Japan 24 (1972), 638–683.CrossRefGoogle Scholar
Sogge, C. D., Concerning the $L^p$ norm of spectral clusters for second-order elliptic operators on compact manifolds, J. Funct. Anal. 77 (1988), 123–138.CrossRefGoogle Scholar
Steiner, R. S., Uniform bounds on sup-norms of holomorphic forms of real weight, Int. J. Number Theory 12 (2016), 1163–1185.CrossRefGoogle Scholar
Steiner, R. S., Supnorm of modular forms of half-integral weight in the weight aspect, Acta Arith. 177 (2017), 201–218.CrossRefGoogle Scholar
Steiner, R. S., Sup-norm of Hecke–Laplace eigenforms on $S^3$, Math. Ann. 377 (2020), 543–553.CrossRefGoogle Scholar
Steiner, R. S., Small diameters and generators for arithmetic lattices in $\mathrm {SL}_2(\mathbb {R})$ and certain Ramanujan graphs, Ramanujan J. 62 (2023), 953–966.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, No. 32 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Sun, H. and Ye, Y., Double first moment for $L(\frac 12,{\rm Sym}^2f\times g)$ by applying Petersson's formula twice, J. Number Theory 202 (2019), 141–159.CrossRefGoogle Scholar
Templier, N., On the sup-norm of Maass cusp forms of large level, Selecta Math. (N.S.) 16 (2010), 501–531.CrossRefGoogle Scholar
Templier, N., Hybrid sup-norm bounds for Hecke–Maass cusp forms, J. Eur. Math. Soc. (JEMS) 17 (2015), 2069–2082.CrossRefGoogle Scholar
VanderKam, J. M., $L^\infty$ norms and quantum ergodicity on the sphere, Int. Math. Res. Not. IMRN 1997 (1997), 329–347.CrossRefGoogle Scholar
Vignéras, M.-F., Séries thêta des formes quadratiques indéfinies, in Séminaire Delange-Pisot-Poitou, 17e année (1975/76), Théorie des nombres: Fasc. 1, Exp. No. 20 (1977), 3, http://www.numdam.org/article/SDPP_1975-1976__17_1_A18_0.pdf.Google Scholar
Voight, J., Quaternion algebras, Graduate Texts in Mathematics, vol. 288 (Springer, Cham, 2021).CrossRefGoogle Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions $L$ automorphes en leur centre de symétrie, Compos. Math. 54 (1985), 173–242.Google Scholar
Watson, T. C., Rankin triple products and quantum chaos, PhD dissertation, Princeton University (2008), arXiv:0810.0425.Google Scholar
Weil, A., Sur certains groupes d'opérateurs unitaires, Acta Math. 111 (1964), 143–211.CrossRefGoogle Scholar
Xia, H., On $L^\infty$ norms of holomorphic cusp forms, J. Number Theory 124 (2007), 325–327.CrossRefGoogle Scholar
Zagier, D., Appendix: The Eichler–Selberg trace formula on $\mathrm {SL}_2(\mathbb {Z})$, in Introduction to modular forms. Grundlehren der mathematischen Wissenschaften, vol. 222 (Springer, Berlin–New York, 1976), 44–55.Google Scholar
Zagier, D., Modular forms whose Fourier coefficients involve zeta-functions of quadratic fields, in Modular functions of one variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics, vol. 627 (Springer, 1977), 105–169.Google Scholar