Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T15:20:28.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Systolic ratio, index of closed orbits and convexity for tight contact forms on the three-sphere

Part of: Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems Symplectic geometry, contact geometry

Published online by Cambridge University Press:  06 November 2018

Alberto Abbondandolo ,
Barney Bramham ,
Umberto L. Hryniewicz  and
Pedro A. S. Salomão
Alberto Abbondandolo
Affiliation:
Ruhr Universität Bochum, Fakultät für Mathematik, Universitätsstrasse 150, D-44801 Bochum, Germany email [email protected]
Barney Bramham
Affiliation:
Ruhr Universität Bochum, Fakultät für Mathematik, Universitätsstrasse 150, D-44801 Bochum, Germany email [email protected]
Umberto L. Hryniewicz
Affiliation:
Universidade Federal do Rio de Janeiro, Departamento de Matemática Aplicada, Av. Athos da Silveira Ramos 149, Rio de Janeiro RJ, 21941-909, Brazil email [email protected]
Pedro A. S. Salomão
Affiliation:
Universidade de São Paulo, Instituto de Matemática e Estatística, Departamento de Matemática, Rua do Matão, 1010 – Cidade Universitária, São Paulo SP, 05508-090, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a dynamically convex contact form on the three-sphere whose systolic ratio is arbitrarily close to 2. This example is related to a conjecture of Viterbo, whose validity would imply that the systolic ratio of a convex contact form does not exceed 1. We also construct, for every integer 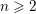$n\geqslant 2$, a tight contact form with systolic ratio arbitrarily close to $n$ and with suitable bounds on the mean rotation number of all the closed orbits of the induced Reeb flow.

Keywords

Reeb dynamicssystolic geometryperiodic orbits

MSC classification

Primary: 53D10: Contact manifolds, general
Secondary: 37J05: General theory, relations with symplectic geometry and topology
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 12 , December 2018 , pp. 2643 - 2680
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of A. Abbondandolo and B. Bramham is supported by the SFB/TRR 191 ‘Symplectic Structures in Geometry, Algebra and Dynamics’, funded by the Deutsche Forschungsgemeinschaft. P. A. S. Salomão is supported by the FAPESP grant 2016/25053-8 and the CNPq grant 306106/2016-7. U. L. Hryniewicz was supported by CNPq grant 309966/2016-7 and by the Humboldt Foundation; he also acknowledges the generous hospitality of the Mathematics Department of the Ruhr-Universität Bochum.

References

Abbondandolo, A., Bramham, B., Hryniewicz, U. L. and Salomão, P. A. S., Sharp systolic inequalities for Reeb flows on the three-sphere , Invent. Math. 211 (2018), 687–778.Google Scholar
Álvarez Paiva, J. C. and Balacheff, F., Contact geometry and isosystolic inequalities , Geom. Funct. Anal. 24 (2014), 648–669.Google Scholar
Artstein-Avidan, S., Karasev, R. and Ostrover, Y., From symplectic measurements to the Mahler conjecture , Duke Math. J. 163 (2014), 2003–2022.Google Scholar
Artstein-Avidan, S., Milman, V. and Ostrover, Y., The M-ellipsoid, symplectic capacities and volume , Comment. Math. Helv. 83 (2008), 359–369.Google Scholar
Clarke, F. H., A classical variational principle for periodic Hamiltonian trajectories , Proc. Amer. Math. Soc. 76 (1979), 186–188.Google Scholar
Ekeland, I., Convexity methods in Hamiltonian systems, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 19 (Springer, Berlin, 1990).Google Scholar
Hofer, H., Pseudoholomorphic curves in symplectizations with applications to the Weinstein conjecture in dimension three , Invent. Math. 114 (1993), 515–563.Google Scholar
Hofer, H., Wysocki, K. and Zehnder, E., The dynamics on three-dimensional strictly convex energy surfaces , Ann. of Math. (2) 148 (1998), 197–289.Google Scholar
Hofer, H. and Zehnder, E., A new capacity for symplectic manifolds, Analysis, et cetera (Academic Press, Boston, MA, 1990), 405–427.Google Scholar
Rabinowitz, P. H., Periodic solutions of Hamiltonian systems , Comm. Pure Appl. Math. 31 (1978), 157–184.Google Scholar
Robbin, J. and Salamon, D., The spectral flow and the Maslov index , Bull. Lond. Math. Soc. 27 (1995), 1–33.Google Scholar
Taubes, C. H., The Seiberg–Witten equations and the Weinstein conjecture , Geom. Topol. 11 (2007), 2117–2202.Google Scholar
Viterbo, C., Metric and isoperimetric problems in symplectic geometry , J. Amer. Math. Soc. 13 (2000), 411–431.Google Scholar