Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Atobe, Hiraku
and
Gan, Wee Teck
2017.
Local theta correspondence of tempered representations and Langlands parameters.
Inventiones mathematicae,
Vol. 210,
Issue. 2,
p.
341.
Krishna, Rahul
2019.
A new proof of the Waldspurger formula, I.
Algebra & Number Theory,
Vol. 13,
Issue. 3,
p.
577.
Emory, Melissa
2020.
On the global Gan–Gross–Prasad conjecture for general spin groups.
Pacific Journal of Mathematics,
Vol. 306,
Issue. 1,
p.
115.
Atobe, Hiraku
2020.
A theory of Miyawaki liftings: the Hilbert–Siegel case.
Mathematische Annalen,
Vol. 376,
Issue. 3-4,
p.
1467.
Haan, Jaeho
2024.
Regularized periods and the global Gan–Gross–Prasad conjecture: the case of $$U(n+2r) \times U(n)$$.
Mathematische Annalen,
Vol. 389,
Issue. 4,
p.
4149.
Wang, Bryan Peng Jun
2025.
Global theta lifting and automorphic periods associated to nilpotent orbits.
Journal of Number Theory,
Vol. 271,
Issue. ,
p.
122.
Atobe, Hiraku
2025.
Local newforms for generic representations of unramified even unitary groups I: Even conductor case.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,
Furusawa, Masaaki
and
Morimoto, Kazuki
2025.
On the Gan–Gross–Prasad conjecture and its refinement for $$\left( \textrm{U}\left( 2n\right) , \textrm{U}\left( 1\right) \right) $$.
Mathematische Annalen,
Vol. 391,
Issue. 3,
p.
3799.
Gan, Wee Teck
and
Wang, Bryan Peng Jun
2025.
Generalised Whittaker models as instances of relative Langlands duality.
Advances in Mathematics,
Vol. 463,
Issue. ,
p.
110129.
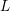 $L$-functions. This identity can be viewed as a refinement to the global Gan–Gross–Prasad conjecture for
$L$-functions. This identity can be viewed as a refinement to the global Gan–Gross–Prasad conjecture for 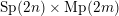 $\text{Sp}(2n)\times \text{Mp}(2m)$. To support this conjectural identity, we show that when
$\text{Sp}(2n)\times \text{Mp}(2m)$. To support this conjectural identity, we show that when 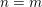 $n=m$ and
$n=m$ and 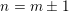 $n=m\pm 1$, it can be deduced from the Ichino–Ikeda conjecture in some cases via theta correspondences. As a corollary, the conjectural identity holds when
$n=m\pm 1$, it can be deduced from the Ichino–Ikeda conjecture in some cases via theta correspondences. As a corollary, the conjectural identity holds when 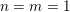 $n=m=1$ or when
$n=m=1$ or when 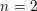 $n=2$,
$n=2$, 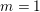 $m=1$ and the automorphic representation on the bigger group is endoscopic.
$m=1$ and the automorphic representation on the bigger group is endoscopic.