Article contents
Rank 3 rigid representations of projective fundamental groups
Published online by Cambridge University Press: 30 May 2018
Abstract
Let
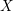 $X$
be a smooth complex projective variety with basepoint
$X$
be a smooth complex projective variety with basepoint
 $x$
. We prove that every rigid integral irreducible representation
$x$
. We prove that every rigid integral irreducible representation
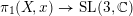 $\unicode[STIX]{x1D70B}_{1}(X\!,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is of geometric origin, i.e., it comes from some family of smooth projective varieties. This partially generalizes an earlier result by Corlette and the second author in the rank 2 case and answers one of their questions.
$\unicode[STIX]{x1D70B}_{1}(X\!,x)\rightarrow \operatorname{SL}(3,\mathbb{C})$
is of geometric origin, i.e., it comes from some family of smooth projective varieties. This partially generalizes an earlier result by Corlette and the second author in the rank 2 case and answers one of their questions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 4
- Cited by


