No CrossRef data available.
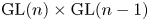 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$Published online by Cambridge University Press: 11 September 2024
We formulate and prove the archimedean period relations for Rankin–Selberg convolutions for 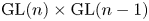 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$. As a consequence, we prove the period relations for critical values of the Rankin–Selberg L-functions for
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$. As a consequence, we prove the period relations for critical values of the Rankin–Selberg L-functions for 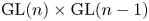 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$ over arbitrary number fields.
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$ over arbitrary number fields.