Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T01:38:57.099Z Has data issue: false hasContentIssue false
  • English
  • Français

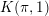On the $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements

Part of: Discrete geometry Projective and enumerative geometry Special aspects of infinite or finite groups Differential algebra

Published online by Cambridge University Press:  20 January 2020

Nils Amend ,
Pierre Deligne  and
Gerhard Röhrle
Nils Amend
Affiliation:
Institut für Algebra, Zahlentheorie und Diskrete Mathematik, Fakultät für Mathematik und Physik, Gottfried Wilhelm Leibniz Universität Hannover, Welfengarten 1, D-30167 Hannover, Germany email [email protected]
Pierre Deligne
Affiliation:
Institute for Advanced Study, 1 Einstein Drive, Princeton, NJ 08540, USA email [email protected]
Gerhard Röhrle
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstraße 150, D-44780 Bochum, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $W\subset \operatorname{GL}(V)$ be a complex reflection group and 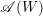$\mathscr{A}(W)$ the set of the mirrors of the complex reflections in 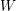$W$. It is known that the complement 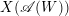$X(\mathscr{A}(W))$ of the reflection arrangement 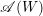$\mathscr{A}(W)$ is a 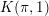$K(\unicode[STIX]{x1D70B},1)$ space. For 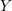$Y$ an intersection of hyperplanes in 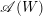$\mathscr{A}(W)$, let 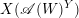$X(\mathscr{A}(W)^{Y})$ be the complement in 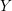$Y$ of the hyperplanes in 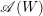$\mathscr{A}(W)$ not containing 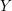$Y$. We hope that 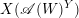$X(\mathscr{A}(W)^{Y})$ is always a $K(\unicode[STIX]{x1D70B},1)$. We prove it in case of the monomial groups 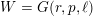$W=G(r,p,\ell )$. Using known results, we then show that there remain only three irreducible complex reflection groups, leading to just eight such induced arrangements for which this 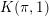$K(\unicode[STIX]{x1D70B},1)$ property remains to be proved.

Keywords

complex reflection groupsreflection arrangementsrestricted arrangementsK (𝜋, 1)-arrangementsEilenberg–MacLane space

MSC classification

Primary: 20F55: Reflection and Coxeter groups 52C35: Arrangements of points, flats, hyperplanes 14N20: Configurations and arrangements of linear subspaces
Secondary: 13N15: Derivations
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 3 , March 2020 , pp. 526 - 532
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amend, N., Möller, T. and Röhrle, G., Restrictions of aspherical arrangements, Topology Appl. 249 (2018), 67–72.CrossRefGoogle Scholar
Bessis, D., Finite complex reflection arrangements are K (𝜋, 1), Ann. of Math. (2) 181 (2015), 809–904.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Groupes et algèbres de Lie. Chapitres IV–VI, Actualités Scientifiques et Industrielles, vol. 1337 (Hermann, Paris, 1968).Google Scholar
Brieskorn, E., Sur les groupes de tresses [d’après V. I. Arnold], in Séminaire Bourbaki, 24ème année (1971/1972), Exp. No. 401, Lecture Notes in Mathematics, vol. 317 (Springer, Berlin, 1973), 21–44.CrossRefGoogle Scholar
Deligne, P., Les immeubles des groupes de tresses généralisés, Invent. Math. 17 (1972), 273–302.CrossRefGoogle Scholar
Ehresmann, C., Sur les espaces fibrés différentiables, C. R. Math. Acad. Sci. Paris 224 (1947), 1611–1612.Google Scholar
Fadell, E. and Neuwirth, L., Configuration spaces, Math. Scand. 10 (1962), 111–118.CrossRefGoogle Scholar
Falk, M. and Randell, R., The lower central series of a fiber-type arrangement, Invent. Math. 82 (1985), 77–88.CrossRefGoogle Scholar
Hattori, A., Topology of ℂn minus a finite number of affine hyperplanes in general position, J. Fac. Sci. Univ. Tokyo 22 (1975), 205–219.Google Scholar
Nakamura, T., A note on the K (𝜋, 1)-property of the orbit space of the unitary reflection group G (m, l, n), Sci. Papers College Arts Sci. Univ. Tokyo 33 (1983), 1–6.Google Scholar
Orlik, P. and Solomon, L., Arrangements defined by unitary reflection groups, Math. Ann. 261 (1982), 339–357.CrossRefGoogle Scholar
Orlik, P. and Solomon, L., Discriminants in the invariant theory of reflection groups, Nagoya Math. J. 109 (1988), 23–45.CrossRefGoogle Scholar
Orlik, P. and Terao, H., Arrangements of hyperplanes (Springer, Berlin, 1992).CrossRefGoogle Scholar
Paris, L., The Deligne complex of a real arrangement of hyperplanes, Nagoya Math. J. 131 (1993), 39–65.CrossRefGoogle Scholar
Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canad. J. Math. 6 (1954), 274–304.CrossRefGoogle Scholar
Terao, H., Modular elements of lattices and topological fibrations, Adv. Math. 62 (1986), 135–154.CrossRefGoogle Scholar