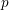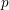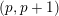Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Xia, Wei
2021.
Deformations of Dolbeault cohomology classes for Lie algebra with complex structures.
Annals of Global Analysis and Geometry,
Vol. 60,
Issue. 3,
p.
709.
Tu, Jie
2021.
The correspondence formula of Dolbeault complex on pair deformation.
Geometriae Dedicata,
Vol. 212,
Issue. 1,
p.
365.
Sferruzza, Tommaso
and
Tardini, Nicoletta
2022.
p-Kähler and balanced structures on nilmanifolds with nilpotent complex structures.
Annals of Global Analysis and Geometry,
Vol. 62,
Issue. 4,
p.
869.
RAO, SHENG
WAN, XUEYUAN
and
ZHAO, QUANTING
2022.
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD -LEMMA.
Nagoya Mathematical Journal,
Vol. 246,
Issue. ,
p.
305.
Sferruzza, Tommaso
2022.
Deformations of balanced metrics.
Bulletin des Sciences Mathématiques,
Vol. 178,
Issue. ,
p.
103143.
Xia, Wei
2022.
Deformations of Dolbeault cohomology classes.
Mathematische Zeitschrift,
Vol. 300,
Issue. 3,
p.
2931.
Cao, Shiyu
2023.
Deformations of Compact Complex Manifolds with Ample Canonical Bundles.
Chinese Annals of Mathematics, Series B,
Vol. 44,
Issue. 1,
p.
1.
Yang, Song
and
Yang, Xiangdong
2023.
Bott-Chern hypercohomology and bimeromorphic invariants.
Complex Manifolds,
Vol. 10,
Issue. 1,
Hind, Richard
Medori, Costantino
and
Tomassini, Adriano
2023.
Families of Almost Complex Structures and Transverse (p, p)-Forms.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 10,
Fino, Anna
and
Mainenti, Asia
2024.
A note on p-Kähler structures on compact quotients of Lie groups.
Annali di Matematica Pura ed Applicata (1923 -),
Cattaneo, Andrea
and
Tomassini, Adriano
2024.
$$\partial \bar{\partial }$$-lemma and p-Kähler structures on families of solvmanifolds.
Mathematische Zeitschrift,
Vol. 308,
Issue. 3,
Wei, Dingchang
and
Zhu, Shengmao
2024.
Two Applications of the $$\partial \overline \partial $$-Hodge Theory.
Chinese Annals of Mathematics, Series B,
Vol. 45,
Issue. 1,
p.
137.
Rao, Sheng
and
Zou, Yongpan
2024.
$$\partial \overline{\partial }$$-Lemma and Double Complex.
Communications in Mathematics and Statistics,
Xia, Tiancheng
2025.
The deformation of the balanced cone and its degeneration.
Differential Geometry and its Applications,
Vol. 98,
Issue. ,
p.
102225.