Published online by Cambridge University Press: 17 July 2014
In this paper we prove a version of curved Koszul duality for 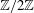 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}$-graded curved coalgebras and their cobar differential graded algebras. A curved version of the homological perturbation lemma is also obtained as a useful technical tool for studying curved (co)algebras and precomplexes. The results of Koszul duality can be applied to study the category of matrix factorizations
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}$-graded curved coalgebras and their cobar differential graded algebras. A curved version of the homological perturbation lemma is also obtained as a useful technical tool for studying curved (co)algebras and precomplexes. The results of Koszul duality can be applied to study the category of matrix factorizations 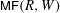 $\mathsf{MF}(R,W)$. We show how Dyckerhoff’s generating results fit into the framework of curved Koszul duality theory. This enables us to clarify the relationship between the Borel–Moore Hochschild homology of curved (co)algebras and the ordinary Hochschild homology of the category
$\mathsf{MF}(R,W)$. We show how Dyckerhoff’s generating results fit into the framework of curved Koszul duality theory. This enables us to clarify the relationship between the Borel–Moore Hochschild homology of curved (co)algebras and the ordinary Hochschild homology of the category 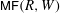 $\mathsf{MF}(R,W)$. Similar results are also obtained in the orbifold case and in the graded case.
$\mathsf{MF}(R,W)$. Similar results are also obtained in the orbifold case and in the graded case.