Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ngoan, Ngô Thị
and
Thǎńg, Nguyêñ Quôć
2019.
On some local–global principles for linear algebraic groups over infinite algebraic extensions of global fields.
Linear Algebra and its Applications,
Vol. 568,
Issue. ,
p.
39.
Colliot-Thélène, J.-L.
Harbater, D.
Hartmann, J.
Krashen, D.
Parimala, R.
and
Suresh, V.
2019.
Local-global principles for zero-cycles on homogeneous spaces over arithmetic function fields.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 8,
p.
5263.
Suresh, Venapally
2020.
Third Galois cohomology group of function fields of curves over number fields.
Algebra & Number Theory,
Vol. 14,
Issue. 3,
p.
701.
Hu, Yong
and
Wu, Zhengyao
2020.
On the Rost divisibility of henselian discrete valuation fields of cohomological dimension 3.
Annals of K-Theory,
Vol. 5,
Issue. 4,
p.
677.
Suresh, Venapally
2020.
Third Galois cohomology group of function fields of curves over number fields.
Algebra & Number Theory,
Vol. 14,
Issue. 3,
p.
701.
Hu, Yong
2020.
Reduced norms of division algebras over complete discrete valuation fields of local-global type.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 11,
p.
2050217.
Mishra, Sumit Chandra
2021.
Local-global principles for norm one tori over semi-global fields.
Mathematische Zeitschrift,
Vol. 298,
Issue. 1-2,
p.
1.
Colliot-Thélène, Jean-Louis
Harbater, David
Hartmann, Julia
Krashen, Daniel
Parimala, R.
and
Suresh, V.
2022.
Local-Global Principles for Constant Reductive Groups over Semi-Global Fields.
Michigan Mathematical Journal,
Vol. 72,
Issue. none,
Gosavi, Saurabh
2022.
Galois cohomology of function fields of curves over non-archimedean local fields.
Proceedings of the American Mathematical Society,
Mishra, Sumit Chandra
2024.
Local-global principles for multinorm tori over semi-global fields.
Israel Journal of Mathematics,
Mehmeti, Vlerë
2024.
An analytic viewpoint on the Hasse principle.
Journal de l’École polytechnique — Mathématiques,
Vol. 11,
Issue. ,
p.
875.
Barlow, Jack
2025.
A local-global principle for similarities over function fields of p-adic curves.
Journal of Algebra,
Vol. 663,
Issue. ,
p.
435.
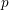 $p$-adic curves
$p$-adic curves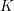 $K$ be a (non-archimedean) local field and let
$K$ be a (non-archimedean) local field and let 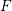 $F$ be the function field of a curve over
$F$ be the function field of a curve over 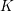 $K$. Let
$K$. Let 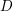 $D$ be a central simple algebra over
$D$ be a central simple algebra over 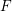 $F$ of period
$F$ of period  $n$ and
$n$ and 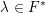 $\unicode[STIX]{x1D706}\in F^{\ast }$. We show that if
$\unicode[STIX]{x1D706}\in F^{\ast }$. We show that if  $n$ is coprime to the characteristic of the residue field of
$n$ is coprime to the characteristic of the residue field of 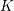 $K$ and
$K$ and 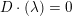 $D\cdot (\unicode[STIX]{x1D706})=0$ in
$D\cdot (\unicode[STIX]{x1D706})=0$ in 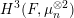 $H^{3}(F,\unicode[STIX]{x1D707}_{n}^{\otimes 2})$, then
$H^{3}(F,\unicode[STIX]{x1D707}_{n}^{\otimes 2})$, then 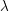 $\unicode[STIX]{x1D706}$ is a reduced norm from
$\unicode[STIX]{x1D706}$ is a reduced norm from 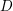 $D$. This leads to a Hasse principle for the group
$D$. This leads to a Hasse principle for the group 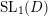 $\operatorname{SL}_{1}(D)$, namely, an element
$\operatorname{SL}_{1}(D)$, namely, an element 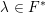 $\unicode[STIX]{x1D706}\in F^{\ast }$ is a reduced norm from
$\unicode[STIX]{x1D706}\in F^{\ast }$ is a reduced norm from 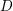 $D$ if and only if it is a reduced norm locally at all discrete valuations of
$D$ if and only if it is a reduced norm locally at all discrete valuations of 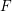 $F$.
$F$.