Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Popov, Vladimir L.
2014.
Automorphisms in Birational and Affine Geometry.
Vol. 79,
Issue. ,
p.
185.
Jelonek, Zbigniew
2015.
On the group of automorphisms of a quasi-affine variety.
Mathematische Annalen,
Vol. 362,
Issue. 1-2,
p.
569.
Prokhorov, Yuri
and
Shramov, Constantin
2018.
‐subgroups in the space Cremona group.
Mathematische Nachrichten,
Vol. 291,
Issue. 8-9,
p.
1374.
Kim, Jin Hong
2018.
Jordan property and automorphism groups of normal compact Kähler varieties.
Communications in Contemporary Mathematics,
Vol. 20,
Issue. 03,
p.
1750024.
Mundet i Riera, Ignasi
2018.
Finite subgroups of Ham and Symp.
Mathematische Annalen,
Vol. 370,
Issue. 1-2,
p.
331.
Prokhorov, Yu. G.
and
Shramov, K. A.
2019.
Automorphism Groups of Moishezon Threefolds.
Mathematical Notes,
Vol. 106,
Issue. 3-4,
p.
651.
Shramov, Constantin
2019.
Fiberwise bimeromorphic maps of conic bundles.
International Journal of Mathematics,
Vol. 30,
Issue. 11,
p.
1950059.
BANDMAN, TATIANA
and
ZARHIN, YURI G.
2019.
JORDAN PROPERTIES OF AUTOMORPHISM GROUPS OF CERTAIN OPEN ALGEBRAIC VARIETIES.
Transformation Groups,
Vol. 24,
Issue. 3,
p.
721.
Prokhorov, Yuri Gennadievich
and
Shramov, Constantin Aleksandrovich
2019.
Группы автоморфизмов трехмерных мойшезоновых многообразий.
Математические заметки,
Vol. 106,
Issue. 4,
p.
636.
Mundet i Riera, Ignasi
2019.
Finite group actions on homology spheres and manifolds with nonzero Euler characteristic.
Journal of Topology,
Vol. 12,
Issue. 3,
p.
744.
Prokhorov, Yu. G.
and
Shramov, C. A.
2020.
Bounded automorphism groups of compact complex surfaces.
Sbornik: Mathematics,
Vol. 211,
Issue. 9,
p.
1310.
Prokhorov, Yu. G.
and
Shramov, C. A.
2020.
Finite groups of bimeromorphic selfmaps of uniruled Kähler threefolds.
Izvestiya: Mathematics,
Vol. 84,
Issue. 5,
p.
978.
Kuznetsova, Alexandra
2020.
Конечные 3-подгруппы в группе Кремоны ранга 3.
Математические заметки,
Vol. 108,
Issue. 5,
p.
725.
Pukhlikov, A. V.
2020.
Birational geometry of singular Fano hypersurfaces of index two.
manuscripta mathematica,
Vol. 161,
Issue. 1-2,
p.
161.
Shramov, Constantin Aleksandrovich
2020.
Неабелевы группы,
действующие на поверхностях Севери-Брауэра.
Математические заметки,
Vol. 108,
Issue. 6,
p.
952.
Prokhorov, Yuri Gennadievich
and
Shramov, Constantin Aleksandrovich
2020.
Конечные группы бимероморфных автоморфизмов унилинейчатых трехмерных кэлеровых многообразий.
Известия Российской академии наук. Серия математическая,
Vol. 84,
Issue. 5,
p.
169.
Javanpeykar, Ariyan
2020.
Arithmetic Geometry of Logarithmic Pairs and Hyperbolicity of Moduli Spaces.
p.
135.
Prokhorov, Yuri Gennadievich
and
Shramov, Constantin Aleksandrovich
2020.
Ограниченные группы автоморфизмов компактных комплексных поверхностей.
Математический сборник,
Vol. 211,
Issue. 9,
p.
105.
GULD, A.
2020.
BOUNDEDNESS PROPERTIES OF AUTOMORPHISM GROUPS OF FORMS OF FLAG VARIETIES.
Transformation Groups,
Vol. 25,
Issue. 4,
p.
1161.
Kuznetsova, A. A.
2020.
Finite 3-Subgroups in the Cremona Group of Rank 3.
Mathematical Notes,
Vol. 108,
Issue. 5-6,
p.
697.
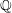 $\mathbb{Q}$ have bounded orders. Further, we investigate which algebraic varieties have groups of birational selfmaps satisfying the Jordan property. Unless explicitly stated otherwise, all varieties are assumed to be algebraic, geometrically irreducible and defined over an arbitrary field
$\mathbb{Q}$ have bounded orders. Further, we investigate which algebraic varieties have groups of birational selfmaps satisfying the Jordan property. Unless explicitly stated otherwise, all varieties are assumed to be algebraic, geometrically irreducible and defined over an arbitrary field 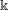 $\Bbbk$ of characteristic zero.
$\Bbbk$ of characteristic zero.