Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T14:59:53.020Z Has data issue: false hasContentIssue false
  • English
  • Français

The generalized Fermat equation with exponents 2, 3, $n$

Part of: Arithmetic problems. Diophantine geometry Diophantine equations Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 November 2019

Nuno Freitas ,
Bartosz Naskręcki  and
Michael Stoll
Nuno Freitas
Affiliation:
Departament de Matemàtiques i Informàtica, Universitat de Barcelona (UB), Gran Via de les Corts Catalanes 585, 08007 Barcelona, Spain email [email protected]
Bartosz Naskręcki
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University in Poznań, Uniwersytetu Poznańskiego 4, 61-614 Poznań, Poland email [email protected]
Michael Stoll
Affiliation:
Mathematisches Institut, Universität Bayreuth, 95440 Bayreuth, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the generalized Fermat equation 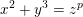$x^{2}+y^{3}=z^{p}$, to be solved in coprime integers, where 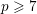$p\geqslant 7$ is prime. Modularity and level-lowering techniques reduce the problem to the determination of the sets of rational points satisfying certain 2-adic and 3-adic conditions on a finite set of twists of the modular curve 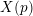$X(p)$. We develop new local criteria to decide if two elliptic curves with certain types of potentially good reduction at 2 and 3 can have symplectically or anti-symplectically isomorphic 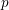$p$-torsion modules. Using these criteria we produce the minimal list of twists of 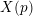$X(p)$ that have to be considered, based on local information at 2 and 3; this list depends on 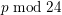$p\hspace{0.2em}{\rm mod}\hspace{0.2em}24$. We solve the equation completely when 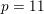$p=11$, which previously was the smallest unresolved 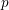$p$. One new ingredient is the use of the ‘Selmer group Chabauty’ method introduced by the third author, applied in an elliptic curve Chabauty context, to determine relevant points on 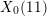$X_{0}(11)$ defined over certain number fields of degree 12. This result is conditional on the generalized Riemann hypothesis, which is needed to show correctness of the computation of the class groups of five specific number fields of degree 36. We also give some partial results for the case 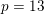$p=13$. The source code for the various computations is supplied as supplementary material with the online version of this article.

Keywords

generalized Fermat equationmodularitysymplectic methodrational pointsSelmer group Chabauty

MSC classification

Primary: 11D41: Higher degree equations; Fermat's equation
Secondary: 11F80: Galois representations 11G05: Elliptic curves over global fields 11G07: Elliptic curves over local fields 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields 14G05: Rational points 14G25: Global ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 1 , January 2020 , pp. 77 - 113
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work reported on in this paper was supported by the Deutsche Forschungsgemeinschaft, grant Sto 299/11-1, in the framework of the Priority Programme SPP 1489. The first author was also partly supported by the grant Proyecto RSME-FBBVA 2015 José Luis Rubio de Francia.

References

Balakrishnan, J. S., Dogra, N., Müller, J. S., Tuitman, J. and Vonk, J., Explicit Chabauty–Kim for the split Cartan modular curve of level 13 , Ann. of Math. (2) 189 (2019), 885–944, doi:10.4007/annals.2019.189.3.6.Google Scholar
Baran, B., An exceptional isomorphism between modular curves of level 13 , J. Number Theory 145 (2014), 273–300, doi:10.1016/j.jnt.2014.05.017; MR 3253304.Google Scholar
Bennett, M. A., Bruni, C. and Freitas, N., Sums of two cubes as twisted perfect powers, revisited , Algebra Number Theory 12 (2018), 959–999, doi:10.2140/ant.2018.12.959; MR 3830208.Google Scholar
Bilu, Y., Parent, P. and Rebolledo, M., Rational points on X 0 +(p r ) , Ann. Inst. Fourier (Grenoble) 63 (2013), 957–984 (in English, with English and French summaries), doi:10.5802/aif.2781; MR 3137477.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language , J. Symbolic Comput. 24 (1997), 235–265. Computational algebra and number theory (London, 1993), doi:10.1006/jsco.1996.0125; MR 1484478.Google Scholar
Brown, D., Primitive integral solutions to x 2 + y 3 = z 10 , Int. Math. Res. Not. IMRN 2012 (2012), 423–436; MR 2876388 (2012k:11036).Google Scholar
Bruin, N., The Diophantine equations x 2 ± y 4 = ±z 6 and x 2 + y 8 = z 3 , Compos. Math. 118 (1999), 305–321, doi:10.1023/A:1001529706709; MR 1711307 (2001d:11035).Google Scholar
Bruin, N., Chabauty methods using elliptic curves , J. reine angew. Math. 562 (2003), 27–49, doi:10.1515/crll.2003.076; MR 2011330 (2004j:11051).Google Scholar
Bruin, N., The primitive solutions to x 3 + y 9 = z 2 , J. Number Theory 111 (2005), 179–189, doi:10.1016/j.jnt.2004.11.008; MR 2124048 (2006e:11040).Google Scholar
Bruin, N., Poonen, B. and Stoll, M., Generalized explicit descent and its application to curves of genus 3 , Forum Math. Sigma 4 (2016), Art. e6, 80 pp, doi:10.1017/fms.2016.1; MR 3482281.Google Scholar
Bruin, N. and Stoll, M., Two-cover descent on hyperelliptic curves , Math. Comp. 78 (2009), 2347–2370, doi:10.1090/S0025-5718-09-02255-8; MR 2521292 (2010e:11059).Google Scholar
Bruin, N. and Stoll, M., The Mordell–Weil sieve: proving non-existence of rational points on curves , LMS J. Comput. Math. 13 (2010), 272–306, doi:10.1112/S1461157009000187; MR 2685127.Google Scholar
Centeleghe, T. G., Integral Tate modules and splitting of primes in torsion fields of elliptic curves , Int. J. Number Theory 12 (2016), 237–248, doi:10.1142/S1793042116500147; MR 3455277.Google Scholar
Chen, I., The Jacobians of non-split Cartan modular curves , Proc. Lond. Math. Soc. (3) 77 (1998), 1–38, doi:10.1112/S0024611598000392; MR 1625491.Google Scholar
Cohen, H., Number theory, Vol. II. Analytic and modern tools, Graduate Texts in Mathematics, vol. 240 (Springer, New York, 2007); MR 2312338.Google Scholar
Cremona, J. E., Algorithms for modular elliptic curves, second edition (Cambridge University Press, Cambridge, 1997); MR 1628193 (99e:11068).Google Scholar
Dahmen, S. R., Classical and modular methods applied to Diophantine equations, PhD thesis, Utrecht University (2008), https://dspace.library.uu.nl/handle/1874/29640.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s last theorem , in Current developments in mathematics, 1995 (Cambridge, MA) (International Press, Cambridge, MA, 1994), 1–154; MR 1474977.Google Scholar
Darmon, H. and Granville, A., On the equations z m = F (x, y) and Ax p + By q = Cz r , Bull. Lond. Math. Soc. 27 (1995), 513–543, doi:10.1112/blms/27.6.513; MR 1348707 (96e:11042).Google Scholar
de Smit, B. and Edixhoven, B., Sur un résultat d’Imin Chen , Math. Res. Lett. 7 (2000), 147–153 (in French, with English and French summaries), doi:10.4310/MRL.2000.v7.n2.a1; MR 1764312.Google Scholar
Dokchitser, T. and Dokchitser, V., Root numbers of elliptic curves in residue characteristic 2 , Bull. Lond. Math. Soc. 40 (2008), 516–524, doi:10.1112/blms/bdn034; MR 2418807.Google Scholar
Dose, V., Fernández, J., González, J. and Schoof, R., The automorphism group of the non-split Cartan modular curve of level 11 , J. Algebra 417 (2014), 95–102, doi:10.1016/j.jalgebra.2014.05.036; MR 3244639.Google Scholar
Edwards, J., A complete solution to X 2 + Y 3 + Z 5 = 0 , J. reine angew. Math. 571 (2004), 213–236, doi:10.1515/crll.2004.043; MR 2070150 (2005e:11035).Google Scholar
Fisher, T., On families of 7- and 11-congruent elliptic curves , LMS J. Comput. Math. 17 (2014), 536–564, doi:10.1112/S1461157014000059; MR 3356045.Google Scholar
Freitas, N., On the Fermat-type equation x 3 + y 3 = z p , Comment. Math. Helv. 91 (2016), 295–304, doi:10.4171/CMH/386; MR 3493372.Google Scholar
Freitas, N. and Kraus, A., An application of the symplectic argument to some Fermat-type equations , C. R. Math. Acad. Sci. Paris 354 (2016), 751–755 (in English, with English and French summaries), doi:10.1016/j.crma.2016.06.002; MR 3528327.Google Scholar
Freitas, N. and Kraus, A., On the symplectic type of isomorphisms of the p-torsion of elliptic curves, Mem. Amer. Math Soc., to appear. Preprint (2019), arXiv:1607.01218.Google Scholar
Freitas, N. and Siksek, S., Fermat’s last theorem over some small real quadratic fields , Algebra Number Theory 9 (2015), 875–895, doi:10.2140/ant.2015.9.875; MR 3352822.Google Scholar
Gérardin, P., Facteurs locaux des algèbres simples de rang 4. I , in Reductive groups and automorphic forms, I (Paris, 1976/1977), Publications Mathématiques de L’Université Paris VII, vol. 1 (Université Paris VII, Paris, 1978), 37–77 (in French); MR 680785.Google Scholar
Halberstadt, E. and Kraus, A., Courbes de Fermat: résultats et problèmes , J. reine angew. Math. 548 (2002), 167–234 (in French, with English summary), doi:10.1515/crll.2002.058; MR 1915212.Google Scholar
Kraus, A., Sur le défaut de semi-stabilité des courbes elliptiques à réduction additive , Manuscripta Math. 69 (1990), 353–385 (in French, with English summary), doi:10.1007/BF02567933; MR 1080288.Google Scholar
Kraus, A. and Oesterlé, J., Sur une question de B. Mazur , Math. Ann. 293 (1992), 259–275 (in French), doi:10.1007/BF01444715; MR 1166121.Google Scholar
Ligozat, G., Courbes modulaires de niveau 11 , in Modular functions of one variable, V (Proc. Second Int. Conf., University of Bonn, Bonn, 1976), Lecture Notes in Mathematics, vol. 601 (Springer, Berlin, 1977), 149–237; (in French); MR 0463118.Google Scholar
The LMFDB Collaboration, The L-functions and modular forms database, 2017, http://www.lmfdb.org.Google Scholar
Loeffler, D. and Weinstein, J., On the computation of local components of a newform , Math. Comp. 81 (2012), 1179–1200, doi:10.1090/S0025-5718-2011-02530-5; MR 2869056.Google Scholar
Loeffler, D. and Weinstein, J., Erratum: ‘On the computation of local components of a newform’ , Math. Comp. 84 (2015), 355–356, doi:10.1090/S0025-5718-2014-02867-6; MR 3266964.Google Scholar
Mazur, B., Rational isogenies of prime degree (with an appendix by D. Goldfeld) , Invent. Math. 44 (1978), 129–162, doi:10.1007/BF01390348; MR 482230 (80h:14022).Google Scholar
Pacetti, A., On the change of root numbers under twisting and applications , Proc. Amer. Math. Soc. 141 (2013), 2615–2628, doi:10.1090/S0002-9939-2013-11532-7; MR 3056552.Google Scholar
Poonen, B., Schaefer, E. F. and Stoll, M., Twists of X (7) and primitive solutions to x 2 + y 3 = z 7 , Duke Math. J. 137 (2007), 103–158, doi:10.1215/S0012-7094-07-13714-1; MR 2309145 (2008i:11085).Google Scholar
Rohrlich, D. E., Elliptic curves and the Weil–Deligne group, Elliptic Curves and Related Topics, vol. 4 (American Mathematical Society, Providence, RI, 1994), 125–157; MR 1260960.Google Scholar
Serre, J.-P. and Tate, J., Good reduction of abelian varieties , Ann. of Math. (2) 88 (1968), 492–517, doi:10.2307/1970722; MR 0236190.Google Scholar
Shimura, G., Introduction to the arithmetic theory of automorphic functions, Publications of the Mathematical Society of Japan, vol. 11 (Princeton University Press, Princeton, NJ, 1994); reprint of the 1971 original; Kanô Memorial Lectures, 1; MR 1291394.Google Scholar
Siksek, S., Explicit Chabauty over number fields , Algebra Number Theory 7 (2013), 765–793, doi:10.2140/ant.2013.7.765; MR 3095226.Google Scholar
Siksek, S. and Stoll, M., The generalised Fermat equation x 2 + y 3 = z 15 , Arch. Math. (Basel) 102 (2014), 411–421, doi:10.1007/s00013-014-0639-z; MR 3254783.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 106, second edition (Springer, Dordrecht, 2009), doi:10.1007/978-0-387-09494-6; MR 2514094.Google Scholar
Stoll, M., Implementing 2-descent for Jacobians of hyperelliptic curves , Acta Arith. 98 (2001), 245–277, doi:10.4064/aa98-3-4; MR 1829626 (2002b:11089).Google Scholar
Stoll, M., Chabauty without the Mordell–Weil group , in Algorithmic and experimental methods in algebra, geometry, and number theory (Springer, Cham, 2017), 623–663; MR 3792746.Google Scholar
Stoll, M., Magma scripts for the computations, http://www.mathe2.uni-bayreuth.de/stoll/magma/index.html#GenFermat.Google Scholar
Weil, A., Über die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen , Math. Ann. 168 (1967), 149–156 (in German); MR 0207658 (34 #7473).Google Scholar
Supplementary material: File

Freitas et al. supplementary material

Freitas et al. supplementary material

Download Freitas et al. supplementary material(File)
File 49.2 KB