Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T13:23:46.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Functorial destackification of tame stacks with abelian stabilisers

Part of: Birational geometry Algebraic geometry: Foundations

Published online by Cambridge University Press:  26 April 2017

Daniel Bergh
Daniel Bergh*
Affiliation:
Institut for Matematiske Fag, Københavns Universitet, Universitetsparken 5, DK-2100 Copenhagen, Denmark email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an algorithm for removing stackiness from smooth, tame Artin stacks with abelian stabilisers by repeatedly applying stacky blow-ups. The construction works over a general base and is functorial with respect to base change and compositions with gerbes and smooth, stabiliser-preserving maps. 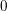As applications, we indicate how the result can be used for destackifying general Deligne–Mumford stacks in characteristic $0$, and to obtain a weak factorisation theorem for such stacks. Over an arbitrary field, the method can be used to obtain a functorial algorithm for desingularising varieties with simplicial toric quotient singularities, without assuming the presence of a toroidal structure.

Keywords

algebraic stacktame stackdestackification

MSC classification

Primary: 14A20: Generalizations (algebraic spaces, stacks) 14E15: Global theory and resolution of singularities
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 6 , June 2017 , pp. 1257 - 1315
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, D., Graber, T. and Vistoli, A., Gromov–Witten theory of Deligne–Mumford stacks , Amer. J. Math. 130 (2008), 1337–1398.Google Scholar
Abramovich, D., Olsson, M. and Vistoli, A., Tame stacks in positive characteristic , Ann. Inst. Fourier (Grenoble) 58 (2008), 1057–1091.CrossRefGoogle Scholar
Bierstone, E. and Milman, P. D., Canonical desingularization in characteristic zero by blowing up the maximum strata of a local invariant , Invent. Math. 128 (1997), 207–302.CrossRefGoogle Scholar
Borisov, L. A., Chen, L. and Smith, G. G., The orbifold Chow ring of toric Deligne–Mumford stacks , J. Amer. Math. Soc. 18 (2005), 193–215.Google Scholar
Buonerba, F., Functorial resolution of tame quotient singularities in positive characteristic, Preprint (2015), arXiv:1511.00550 [math.AG].Google Scholar
Cadman, C., Using stacks to impose tangency conditions on curves , Amer. J. Math. 129 (2007), 405–427.Google Scholar
Cohen, H., A course in computational algebraic number theory, Graduate Texts in Mathematics, vol. 138 (Springer, Heidelberg, 1993).CrossRefGoogle Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, vol. 124 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Dieudonné, J. and Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV , Publ. Math. Inst. Hautes Études Sci. 32 (1967), 5–361.Google Scholar
Edidin, D. and More, Y., Partial desingularizations of good moduli spaces of Artin toric stacks , Michigan Math. J. 61 (2012), 451–474.Google Scholar
Fantechi, B., Mann, E. and Nironi, F., Smooth toric Deligne–Mumford stacks , J. reine angew. Math. 648 (2010), 201–244.Google Scholar
Geraschenko, A. and Satriano, M., Toric stacks I: the theory of stacky fans , Trans. Amer. Math. Soc. 367 (2015), 1033–1071.CrossRefGoogle Scholar
Geraschenko, A. and Satriano, M., Toric stacks II: intrinsic characterization of toric stacks , Trans. Amer. Math. Soc. 367 (2015), 1073–1094.CrossRefGoogle Scholar
Giraud, J., Cohomologie non abélienne, Grundlehren der mathematischen Wissenschaften, Band 179 (Springer, Berlin, 1971).Google Scholar
Gross, P., Tensor generators on schemes and stacks, Preprint (2013), arXiv:1306.5418 [math.AG].Google Scholar
Hausen, J., Equivariant embeddings into smooth toric varieties , Canad. J. Math. 54 (2002), 554–570.CrossRefGoogle Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. I , Ann. of Math. (2) 79 (1964), 109–203.Google Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. II , Ann. of Math. (2) 79 (1964), 205–326.Google Scholar
Iwanari, I., The category of toric stacks , Compos. Math. 145 (2009), 718–746.Google Scholar
Iwanari, I., Logarithmic geometry, minimal free resolutions and toric algebraic stacks , Publ. Math. Inst. Hautes Études Sci. 45 (2009), 1095–1140.Google Scholar
Keel, S. and Mori, S., Quotients by groupoids , Ann. of Math. (2) 145 (1997), 193–213.Google Scholar
Kempf, G., Knudsen, F. F., Mumford, D. and Saint-Donat, B., Toroidal embeddings I, Lecture Notes in Mathematics, vol. 339 (Springer, Heidelberg, 1973).Google Scholar
Kollár, J., Lectures on resolution of singularities, Annals of Mathematics Studies, vol. 166 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Matsuki, K. and Olsson, M., Kawamata–Viehweg vanishing as Kodaira vanishing for stacks , Math. Res. Lett. 12 (2005), 207–217.Google Scholar
Reichstein, Z. and Youssin, B., Essential dimensions of algebraic groups and a resolution theorem for G-varieties , Canad. J. Math. 52 (2000), 1018–1056; with an appendix by János Kollár and Endre Szabó.Google Scholar
Rydh, D., Étale dévissage, descent and pushouts of stacks , J. Algebra 331 (2011), 194–223.CrossRefGoogle Scholar
Rydh, D., Existence and properties of geometric quotients , J. Algebraic Geom. 22 (2013), 629–669.Google Scholar
Satriano, M., The Chevalley–Shephard–Todd theorem for finite linearly reductive group schemes , Algebra Number Theory 6 (2012), 1–26.Google Scholar
Illusie, L., Existence de résolutions globales , in Théorie des intersections et théorème de Riemann–Roch (SGA6), Lecture Notes in Mathematics, vol. 225 (Springer, 1971), 160–221.Google Scholar
The Stacks Project Authors, Stacks project (2017), http://stacks.math.columbia.edu.Google Scholar
Vistoli, A., Intersection theory on algebraic stacks and on their moduli spaces , Invent. Math. 97 (1989), 613–670.Google Scholar
Włodarczyk, J., Birational cobordisms and factorization of birational maps , J. Algebraic Geom. 9 (2000), 425–449.Google Scholar