Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:36:56.486Z Has data issue: false hasContentIssue false
  • English
  • Français

A finiteness theorem on symplectic singularities

Part of: Singularities Families, fibrations Symplectic geometry, contact geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  15 April 2016

Yoshinori Namikawa
Yoshinori Namikawa*
Affiliation:
Department of Mathematics, Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An affine symplectic singularity 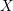$X$ with a good 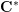$\mathbf{C}^{\ast }$-action is called a conical symplectic variety. In this paper we prove the following theorem. For fixed positive integers 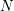$N$ and 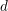$d$, there are only a finite number of conical symplectic varieties of dimension 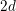$2d$ with maximal weights 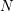$N$, up to an isomorphism. To prove the main theorem, we first relate a conical symplectic variety with a log Fano Kawamata log terminal (klt) pair, which has a contact structure. By the boundedness result for log Fano klt pairs with fixed Cartier index, we prove that conical symplectic varieties of a fixed dimension and with a fixed maximal weight form a bounded family. Next we prove the rigidity of conical symplectic varieties by using Poisson deformations.

Keywords

conical symplectic varietyPoisson deformationcontact Fano orbifold

MSC classification

Primary: 14D15: Formal methods; deformations 14J17: Singularities 14J45: Fano varieties 32S30: Deformations of singularities; vanishing cycles 53D10: Contact manifolds, general 53D17: Poisson manifolds; Poisson groupoids and algebroids
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 6 , June 2016 , pp. 1225 - 1236
Copyright
© The Author 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M., Algebraic approximation of structures over complete local rings, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 23–58.Google Scholar
Beauville, A., Symplectic singularities, Invent. Math. 139 (2000), 541–549.Google Scholar
Braden, T., Licata, A., Proudfoot, N. and Webster, B., Quantizations of conical symplectic resolutions II: Category ${\mathcal{O}}$and symplectic duality, Astérisque, to appear; arXiv:1407.0964.Google Scholar
Braden, T., Proudfoot, N. and Webster, B., Quantizations of conical symplectic resolutions I: Local and global structure, Astérisque, to appear; arXiv:1208.3863.Google Scholar
Collingwood, D. and McGovern, W., Nilpotent orbits in semi-simple Lie algebras (Van Nostrand Reinhold, New York, 1993).Google Scholar
Elkik, R., Singulatités rationnelles et déformations, Invent. Math. 47 (1978), 139–147.CrossRefGoogle Scholar
Hacon, C., McKernan, J. and Xu, C., ACC for log canonical thresholds, Ann. of Math. (2) 180 (2014), 523–571.Google Scholar
Kempf, G., Knudsen, F., Mumford, D. and Saint-Donat, B., Toroidal embeddings I, Lecture Notes in Mathematics, vol. 339 (Springer, Berlin, 1973).Google Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5 (Oxford University Press, London, 1970).Google Scholar
Mumford, D., Towards an enumerative geometry of moduli spaces of curves, in Arithmetic and geometry, eds Artin, M. and Tate, J. (Birkhäuser, Boston, 1983), 271–326.CrossRefGoogle Scholar
Mumford, D., Lectures on curves on an algebraic surface, Annals of Mathematical Studies, vol. 59 (Princeton University Press, Princeton, NJ, 1966).Google Scholar
Nakajima, H., Instantons on ALE spaces, quiver varieties, and Kac–Moody algebras, Duke Math. J. 76 (1994), 365–416.Google Scholar
Namikawa, Y., Poisson deformations of affine symplectic varieties, Duke Math. J. 156 (2011), 51–85.Google Scholar
Namikawa, Y., Equivalence of symplectic singularities, Kyoto J. Math. 53(2) (2013), 483–514.CrossRefGoogle Scholar
Namikawa, Y., Fundamental groups of symplectic singularities, Adv. Stud. Pure Math., to appear; arXiv:1301.1008.Google Scholar
Namikawa, Y., On the structure of homogeneous symplectic varieties of complete intersection, Invent. Math. 193 (2013), 159–185.CrossRefGoogle Scholar
Slodowy, P., Simple singularities and simple algebraic groups, Lecture Notes in Mathematics, vol. 815 (Springer, New York, 1980).Google Scholar