Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T14:31:24.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Équivalence motivique des groupes algébriques semisimples

Part of: Cycles and subschemes Special varieties Linear algebraic groups and related topics

Published online by Cambridge University Press:  27 July 2017

Charles De Clercq
Charles De Clercq*
Affiliation:
LAGA, UMR 7539, Institut Galilée, Université Paris 13, 93430 Villetaneuse, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the standard motives of a semisimple algebraic group 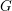$G$ with coefficients in a field of order 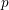$p$ are determined by the upper motives of the group 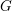$G$. As a consequence of this result, we obtain a partial version of the motivic rigidity conjecture of special linear groups. The result is then used to construct the higher indexes which characterize the motivic equivalence of semisimple algebraic groups. The criteria of motivic equivalence derived from the expressions of these indexes produce a dictionary between motives, algebraic structures and the birational geometry of twisted flag varieties. This correspondence is then described for special linear groups and orthogonal groups (the criteria associated with other groups being obtained in De Clercq and Garibaldi [Tits$p$-indexes of semisimple algebraic groups, J. Lond. Math. Soc. (2) 95 (2017) 567–585]). The proofs rely on the Levi-type motivic decompositions of isotropic twisted flag varieties due to Chernousov, Gille and Merkurjev, and on the notion of pondered field extensions.

On prouve dans cet article que l’ensemble des motifs standards d’un groupe semisimple $G$ à coefficients dans un corps à 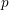$p$ éléments est déterminé par l’ensemble des motifs supérieurs du groupe $G$. En conséquence de ce résultat, on obtient une version partielle de la conjecture de rigidité motivique des groupes spéciaux linéaires. Ce résultat est ensuite utilisé pour construire les indices supérieurs qui caractérisent l’équivalence motivique des groupes semisimples. Les critères d’équivalence motivique dérivés de l’expression de ces indices fournissent un dictionnaire mêlant motifs, structures algébriques et géométrie birationnelle des variétés de drapeaux généralisées. Cette correspondance est ensuite décrite pour les groupes spéciaux linéaires et les groupes orthogonaux (les critères afférents pour les autres groupes faisant l’objet de De Clercq and Garibaldi [Tits$p$-indexes of semisimple algebraic groups, J. Lond. Math. Soc. (2) 95 (2017) 567–585]). Les preuves de ces résultats reposent principalement sur les décompositions motiviques de type Levi de Chernousov, Gille et Merkurjev des variétés de drapeaux isotropes, ainsi que sur la notion d’extension pondérée.

Keywords

motivessemisimple groupsflag varieties

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives 14M15: Grassmannians, Schubert varieties, flag manifolds 20G15: Linear algebraic groups over arbitrary fields
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 10 , October 2017 , pp. 2195 - 2213
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, H. and Ohm, J., Function fields of Pfister neighbors , J. Algebra 178 (1995), 653–664.Google Scholar
Amitsur, S., Generic splitting fields of central simple algebras , Ann. of Math. (2) 62 (1955), 8–43.CrossRefGoogle Scholar
Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).CrossRefGoogle Scholar
Borel, A. and Springer, T. A., Rationality properties of linear algebraic groups II , Tohoku Math. J. 20 (1968), 443–497.Google Scholar
Borel, A. and Tits, J., Groupes réductifs , Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–151.Google Scholar
Bourbaki, N., Éléments de mathématique , in Groupes et algèbres de Lie (Masson, Paris, 1981), chs 4, 5 and 6.Google Scholar
Brosnan, P., On motivic decompositions arising from the method of Bia lynicki-Birula , Invent. Math. 161 (2005), 91–111.Google Scholar
Calmès, B., Semenov, N., Petrov, V. and Zainoulline, K., Chow motives of twisted flag varieties , Compositio Math. 142 (2006), 1063–1080.CrossRefGoogle Scholar
Chernousov, V., Gille, S. and Merkurjev, A., Motivic decomposition of isotropic projective homogeneous varieties , Duke Math. J. 126 (2005), 137–159.CrossRefGoogle Scholar
Chernousov, V. and Merkurjev, A., Motivic decomposition of projective homogeneous varieties and the Krull–Schmidt theorem , Transform. Groups 11 (2006), 371–386.CrossRefGoogle Scholar
De Clercq, C., Motivic decompositions of projective homogeneous varieties and change of coefficients , C. R. Math. Acad. Sci. Paris 348 (2010), 955–958.Google Scholar
De Clercq, C., Classification of upper motives of algebraic groups of inner type A n , C. R. Math. Acad. Sci. Paris 349 (2011), 433–436.CrossRefGoogle Scholar
De Clercq, C., Motivic rigidity of Severi–Brauer varieties , J. Algebra 373 (2013), 30–38.Google Scholar
De Clercq, C. and Garibaldi, S., Tits p-indexes of semisimple algebraic groups , J. Lond. Math. Soc. (2) 95 (2017), 567–585.CrossRefGoogle Scholar
Elman, R., Karpenko, N. and Merkurjev, A., The algebraic and geometric theory of quadratic forms, AMS Colloquium Publications, vol. 56 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 2 (Springer, Berlin, 1998).CrossRefGoogle Scholar
Garibaldi, S., Petrov, V. and Semenov, N., Shells of twisted flag varieties and the Rost invariant , Duke Math. J. 165 (2016), 285–339.Google Scholar
Grothendieck, A., La torsion homologique et les sections rationnelles, Anneaux de Chow et applications, Exposé 5, Séminaire C. Chevalley, 1958.Google Scholar
Haution, O., Lifting of coefficients for Chow motives of quadrics , in Quadratic forms, linear algebraic groups, and cohomology, Developments in Mathematics, vol. 18 (Springer, New York, 2010), 239–247.Google Scholar
Hoffmann, D. W., Similarity of quadratic forms and half-neighbors , J. Algebra 204 (1998), 255–280.Google Scholar
Hoffmann, D. W., Motivic equivalence and similarity of quadratic forms , Doc. Math. Extra Volume (2015), 265–275.Google Scholar
Izhboldin, O., Motivic equivalence of quadratic forms , Doc. Math. 3 (1998), 341–351.CrossRefGoogle Scholar
Kahn, B., Formes quadratiques et cycles algébriques [d’après Rost, Voevodsky, Vishik, Karpenko …], Exposé Bourbaki no. 941 , Astérisque 307 (2006), 113–163.Google Scholar
Kahn, B., Formes quadratiques sur un corps, Cours spécialisé no. 15, SMF, 2008.Google Scholar
Karpenko, N., Criteria of motivic equivalence for quadratic forms and central simple algebras , Math. Ann. 317 (2000), 585–611.Google Scholar
Karpenko, N., On the first Witt index of quadratic forms , Invent. Math. 153 (2003), 455–462.Google Scholar
Karpenko, N., Canonical dimension , in Proc. int. congress of mathematicians (ICM 2010), Vol. II (Hindustan Book Agency, New Delhi, India, 2010), 146–161.Google Scholar
Karpenko, N., Upper motives of outer algebraic groups , in Quadratic forms, linear algebraic groups, and cohomology, Developments in Mathematics, vol. 18 (Springer, New York, 2010), 249–258.Google Scholar
Karpenko, N., Sufficiently generic orthogonal grassmannians , J. Algebra 372 (2012), 365–375.CrossRefGoogle Scholar
Karpenko, N., Upper motives of algebraic groups and incompressibility of Severi–Brauer varieties , J. Reine Angew. Math. 677 (2013), 179–198.Google Scholar
Kersten, I. and Rehmann, U., Generic splitting of reductive groups , Tohoku Math. J. 46 (1994), 35–70.Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M. and Tignol, J.-P., The book of involutions, with a preface by J. Tits, AMS Colloquium Publications, vol. 44 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Köck, B., Chow motif and higher Chow theory of G/P , Manuscripta Math. 70 (1991), 363–372.CrossRefGoogle Scholar
Lam, T. Y., Introduction to quadratic forms over fields, Graduate Studies in Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Manin, Yu. I., Correspondence, motifs, and monoidal transformations , Mat. Sb. 77 (1968), 475–507; English transl.: Math. USSR-Sb. 6 (1968), 439–470.Google Scholar
Merkurjev, A., Panin, A. and Wadsworth, A., Index reduction formulas for twisted flag varieties I , J. K-Theory 10 (1996), 517–596.Google Scholar
Merkurjev, A., Panin, A. and Wadsworth, A., Index reduction formulas for twisted flag varieties II , J. K-Theory 14 (1998), 101–196.Google Scholar
Petrov, V. and Semenov, N., Generically split projective homogeneous varieties, with an appendix by M. Florence , Duke Math. J. 152 (2010), 155–173.Google Scholar
Petrov, V. and Semenov, N., Generically split projective homogeneous varieties II , J. K-Theory 10 (2010), 1–8.Google Scholar
Petrov, V., Semenov, N. and Zainoulline, K., J-invariant of linear algebraic groups , Ann. Sci. Éc. Norm. Supér. (4) 41 (2008), 1023–1053.CrossRefGoogle Scholar
Quéguiner-Mathieu, A., Semenov, N. and Zainoulline, K., J. Pure Appl. Algebra 216 (2012), 2614–2628.CrossRefGoogle Scholar
Roussey, S., Corps de fonctions et équivalences birationnelles des formes quadratiques, Doctoral Thesis, Université de Franche-Comté (2005).Google Scholar
Demazure, M. and Grothendieck (eds), A., Schémas en groupes. II : Groupes de type multiplicatif, et structure des schémas en groupes généraux. Séminaire de Géométrie Algébrique du Bois Marie 1962/64 (SGA 3). Dirigé par M. Demazure et A. Grothendieck. Lecture Notes in Mathematics, vol. 152 (Springer, Berlin, 1970); MR 274459.Google Scholar
Springer, T. A., Sur les formes quadratiques d’indice zéro , C. R. Acad. Sci. Paris 234 (1952), 1517–1519.Google Scholar
Tits, J., Classification of algebraic semisimple groupsm , in Algebraic groups and discontinuous subgroups, Proceedings of Symposia in Pure Mathematics, vol. 9 (American Mathematical Society, Providence, RI, 1966), 33–62.Google Scholar
Tits, J., Sur les degrés des extensions de corps déployant les groupes algébriques simples , C. R. Acad. Sci. Paris 315 (1992), 1131–1138.Google Scholar
Vishik, A., Motives of quadrics with applications to the theory of quadratic forms , in Geometric methods in the algebraic theory of quadratic forms, Lecture Notes in Mathematics, vol. 1835 (Springer, 2004), 25–101.Google Scholar
Vishik, A., Fields of u-invariant 2 r + 1 , in Algebra, arithmetic and geometry – in honor of Yu. I. Manin (Birkhäuser, Boston, MA, 2010), 661–685.Google Scholar
Vishik, A. and Yagita, N., Algebraic cobordisms of a Pfister quadric , J. Lond. Math. Soc. (2) 76 (2007), 586–604.Google Scholar
Weil, A., Algebras with involutions and the classical groups , J. Indian Math. Soc. (N.S.) 24 (1961), 589–623.Google Scholar
Zhykhovich, M., Decompositions of motives of generalized Severi–Brauer varieties , Doc. Math. 17 (2012), 151–165.CrossRefGoogle Scholar