Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-11T07:47:28.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Equations of hyperelliptic Shimura curves

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  19 January 2017

Jia-Wei Guo  and
Yifan Yang
Jia-Wei Guo
Affiliation:
Institute of Mathematics, Academia Sinica, Taipei, Taiwan 300 email [email protected]
Yifan Yang
Affiliation:
Department of Applied Mathematics, National Chiao Tung University, Hsinchu, Taiwan 300 National Center for Theoretical Sciences, Taipei, Taiwan 106 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By constructing suitable Borcherds forms on Shimura curves and using Schofer’s formula for norms of values of Borcherds forms at CM points, we determine all of the equations of hyperelliptic Shimura curves 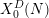$X_{0}^{D}(N)$. As a byproduct, we also address the problem of whether a modular form on Shimura curves 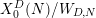$X_{0}^{D}(N)/W_{D,N}$ with a divisor supported on CM divisors can be realized as a Borcherds form, where 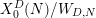$X_{0}^{D}(N)/W_{D,N}$ denotes the quotient of 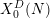$X_{0}^{D}(N)$ by all of the Atkin–Lehner involutions. The construction of Borcherds forms is done by solving certain integer programming problems.

Keywords

Borcherds formsShimura curves

MSC classification

Primary: 11F03: Modular and automorphic functions
Secondary: 11G15: Complex multiplication and moduli of abelian varieties 11G18: Arithmetic aspects of modular and Shimura varieties
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 1 , January 2017 , pp. 1 - 40
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsina, M. and Bayer, P., Quaternion orders, quadratic forms, and Shimura curves , CRM Monograph Series, vol. 22 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Barnard, A. G., The singular theta correspondence, Lorentzian lattices and Borcherds–Kac–Moody algebras, PhD thesis, University of California, Berkeley, ProQuest LLC, Ann Arbor, MI (2003).Google Scholar
Borcherds, R. E., Automorphic forms with singularities on Grassmannians , Invent. Math. 132 (1998), 491–562.CrossRefGoogle Scholar
Borcherds, R. E., Reflection groups of Lorentzian lattices , Duke Math. J. 104 (2000), 319–366.Google Scholar
Boutot, J.-F. and Carayol, H., Uniformisation p-adique des courbes de Shimura: les théorèmes de Čerednik et de Drinfel’d , Astérisque 196–197 (1992), 45–158; 1991. Courbes modulaires et courbes de Shimura (Orsay, 1987/1988).Google Scholar
Bruinier, J. H., Borcherds products on O(2, l) and Chern classes of Heegner divisors , Lecture Notes in Mathematics, vol. 1780 (Springer, Berlin, 2002).Google Scholar
Bruinier, J. H., On the converse theorem for Borcherds products , J. Algebra 397 (2014), 315–342.Google Scholar
Bruinier, J. and Ono, K., Heegner divisors, L-functions and harmonic weak Maass forms , Ann. of Math. (2) 172 (2010), 2135–2181.Google Scholar
Cremona, J. E., Algorithms for modular elliptic curves, second edition (Cambridge University Press, Cambridge, 1997).Google Scholar
Elkies, N. D., Shimura curve computations , in Algorithmic number theory (Portland, OR, 1998), Lecture Notes in Computer Science, vol. 1423 (Springer, Berlin, 1998), 1–47.Google Scholar
Elkies, N. D., Shimura curve computations via K3 surfaces of Néron–Severi rank at least 19 , in Algorithmic number theory, Lecture Notes in Computer Science, vol. 5011 (Springer, Berlin, 2008), 196–211.Google Scholar
Errthum, E., Singular moduli of Shimura curves , Canad. J. Math. 63 (2011), 826–861.Google Scholar
Galbraith, S. D., Equations for modular curves, PhD thesis, University of Oxford (1996).Google Scholar
González, J. and Molina, S., The kernel of Ribet’s isogeny for genus three Shimura curves , J. Math. Soc. Japan 68 (2016), 609–635.Google Scholar
González, J. and Rotger, V., Equations of Shimura curves of genus two , Int. Math. Res. Not. IMRN 2004 (2004), 661–674.CrossRefGoogle Scholar
González, J. and Rotger, V., Non-elliptic Shimura curves of genus one , J. Math. Soc. Japan 58 (2006), 927–948.CrossRefGoogle Scholar
Gross, B. H. and Zagier, D. B., On singular moduli , J. Reine Angew. Math. 355 (1985), 191–220.Google Scholar
Heim, B. and Murase, A., A characterization of holomorphic Borcherds lifts by symmetries , Int. Math. Res. Not. IMRN 2015 (2015), 11150–11185.Google Scholar
Ihara, Y., Congruence relations and Shimūra curves , in Automorphic forms, representations and L-functions (Proceedings of Symposia in Pure Mathematics, Oregon State Univ., Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 291–311.Google Scholar
Jordan, B. W., On the diophantine arithmetic of Shimura curves, PhD thesis, Harvard University, ProQuest LLC, Ann Arbor, MI (1981).Google Scholar
Katok, S., Fuchsian groups , Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1992).Google Scholar
Kudla, S. S., Integrals of Borcherds forms , Compositio Math. 137 (2003), 293–349.CrossRefGoogle Scholar
Kurihara, A., On some examples of equations defining Shimura curves and the Mumford uniformization , J. Fac. Sci. Univ. Tokyo Sect. IA Math. 25 (1979), 277–300.Google Scholar
Molina, S., Equations of hyperelliptic Shimura curves , Proc. Lond. Math. Soc. (3) 105 (2012), 891–920.CrossRefGoogle Scholar
Ogg, A. P., Real points on Shimura curves , in Arithmetic and geometry, Vol. I, Progress in Mathematics, vol. 35 (Birkhäuser, Boston, MA, 1983), 277–307.Google Scholar
Schofer, J., Borcherds forms and generalizations of singular moduli , J. Reine Angew. Math. 629 (2009), 1–36.Google Scholar
Serre, J.-P. and Stark, H. M., Modular forms of weight 1/2 , in Modular functions of one variable, VI (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics, vol. 627 (Springer, Berlin, 1977), 27–67.Google Scholar
Tu, F.-T., Schwarzian differential equations associated to Shimura curves of genus zero , Pacific J. Math. 269 (2014), 453–489.Google Scholar
Yang, Y., Defining equations of modular curves , Adv. Math. 204 (2006), 481–508.Google Scholar
Yang, Y., Special values of hypergeometric functions and periods of CM elliptic curves, Preprint (2015), arXiv:1503.07971 [math.NT].Google Scholar
Zhang, S., Heights of Heegner points on Shimura curves , Ann. of Math. (2) 153 (2001), 27–147.Google Scholar