Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Konno, Hitoshi
2018.
Elliptic stable envelopes and finite-dimensional representations of elliptic quantum group.
Journal of Integrable Systems,
Vol. 3,
Issue. 1,
Ando, Matthew
Blumberg, Andrew
and
Gepner, David
2018.
Parametrized spectra, multiplicative Thom spectra and the twisted Umkehr map.
Geometry & Topology,
Vol. 22,
Issue. 7,
p.
3761.
Rimányi, R.
Tarasov, V.
and
Varchenko, A.
2019.
Elliptic and K-theoretic stable envelopes and Newton polytopes.
Selecta Mathematica,
Vol. 25,
Issue. 1,
Rezk, Charles
2020.
Looijenga line bundles in complex analytic elliptic cohomology.
Tunisian Journal of Mathematics,
Vol. 2,
Issue. 1,
p.
1.
Rimányi, Richárd
and
Weber, Andrzej
2020.
Elliptic classes of Schubert varieties via Bott–Samelson resolution.
Journal of Topology,
Vol. 13,
Issue. 3,
p.
1139.
Kumar, Shrawan
Rimányi, Richárd
and
Weber, Andrzej
2020.
Elliptic classes of Schubert varieties.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
703.
Aganagic, Mina
and
Okounkov, Andrei
2020.
Elliptic stable envelopes.
Journal of the American Mathematical Society,
Vol. 34,
Issue. 1,
p.
79.
Smirnov, Andrey
2020.
Elliptic stable envelope for Hilbert scheme of points in the plane.
Selecta Mathematica,
Vol. 26,
Issue. 1,
Konno, Hitoshi
2020.
Elliptic Quantum Groups.
Vol. 37,
Issue. ,
p.
87.
Mikosz, Małgorzata
and
Weber, Andrzej
2021.
Elliptic classes, McKay correspondence and theta identities.
Journal of Algebraic Combinatorics,
Vol. 53,
Issue. 3,
p.
701.
Berwick-Evans, Daniel
and
Tripathy, Arnav
2021.
A de Rham model for complex analytic equivariant elliptic cohomology.
Advances in Mathematics,
Vol. 380,
Issue. ,
p.
107575.
Spong, Matthew
2021.
A construction of complex analytic elliptic cohomology from double free loop spaces.
Compositio Mathematica,
Vol. 157,
Issue. 8,
p.
1853.
Okounkov, Andrei
2021.
Inductive construction of stable envelopes.
Letters in Mathematical Physics,
Vol. 111,
Issue. 6,
Rimányi, Richárd
Smirnov, Andrey
Zhou, Zijun
and
Varchenko, Alexander
2022.
Three-Dimensional Mirror Symmetry and Elliptic Stable Envelopes.
International Mathematics Research Notices,
Vol. 2022,
Issue. 13,
p.
10016.
Dinkins, Hunter
2022.
3d mirror symmetry of the cotangent bundle of the full flag variety.
Letters in Mathematical Physics,
Vol. 112,
Issue. 5,
Smirnov, Andrey
and
Zhou, Zijun
2022.
3d mirror symmetry and quantum K-theory of hypertoric varieties.
Advances in Mathematics,
Vol. 395,
Issue. ,
p.
108081.
Bullimore, Mathew
and
Zhang, Daniel
2022.
3d $\mathcal{N}=4$ Gauge Theories on an Elliptic Curve.
SciPost Physics,
Vol. 13,
Issue. 1,
Finkelberg, Michael
Matviichuk, Mykola
and
Polishchuk, Alexander
2022.
Elliptic zastava.
Journal of Algebraic Geometry,
Vol. 32,
Issue. 2,
p.
183.
Zhao, Gufang
and
Zhong, Changlong
2022.
Representations of the elliptic affine Hecke algebras.
Advances in Mathematics,
Vol. 395,
Issue. ,
p.
108077.
Dinkins, Hunter
2023.
Elliptic Stable Envelopes of Affine Type A Quiver Varieties.
International Mathematics Research Notices,
Vol. 2023,
Issue. 15,
p.
13426.
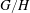 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G/H$, where
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G/H$, where 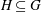 $H\subseteq G$ are compact connected Lie groups of equal rank. We identify the
$H\subseteq G$ are compact connected Lie groups of equal rank. We identify the 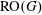 ${\rm RO}(G)$-graded coefficients
${\rm RO}(G)$-graded coefficients 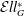 ${\mathcal{E}} ll_G^*$ as powers of Looijenga’s line bundle and prove that transfer along the map
${\mathcal{E}} ll_G^*$ as powers of Looijenga’s line bundle and prove that transfer along the map 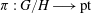 $$\begin{equation*} \pi \,{:}\,G/H\longrightarrow {\rm pt} \end{equation*}$$
$$\begin{equation*} \pi \,{:}\,G/H\longrightarrow {\rm pt} \end{equation*}$$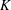 $K$-theory and elliptic cohomology in parallel, this paper organizes the theoretical framework for the elliptic Schubert calculus of [N. Ganter and A. Ram, Elliptic Schubert calculus, in preparation].
$K$-theory and elliptic cohomology in parallel, this paper organizes the theoretical framework for the elliptic Schubert calculus of [N. Ganter and A. Ram, Elliptic Schubert calculus, in preparation].