Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T20:46:20.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformations of the Lie–Poisson sphere of a compact semisimple Lie algebra

Part of: Lie groups Symplectic geometry, contact geometry

Published online by Cambridge University Press:  27 March 2014

Ioan Mărcuț
Ioan Mărcuț*
Affiliation:
University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A compact semisimple Lie algebra 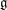$\mathfrak{g}$ induces a Poisson structure 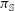$\pi _{\mathbb{S}}$ on the unit sphere 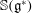$\mathbb{S}(\mathfrak{g}^*)$ in 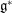$\mathfrak{g}^*$. We compute the moduli space of Poisson structures on 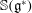$\mathbb{S}(\mathfrak{g}^*)$ around 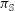$\pi _{\mathbb{S}}$. This is the first explicit computation of a Poisson moduli space in dimension greater or equal than three around a degenerate (i.e. not symplectic) Poisson structure.

Keywords

Poisson geometrysemisimple Lie algebras of compact type

MSC classification

Secondary: 53D17: Poisson manifolds; Poisson groupoids and algebroids 22E15: General properties and structure of real Lie groups
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 4 , April 2014 , pp. 568 - 578
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Borel, A., Sur la cohomologie des espaces fibrés principaux et des espaces homogénes de groupes de Lie compacts, Ann. of Math. (2) 57 (1953), 115–207.CrossRefGoogle Scholar
Crainic, M. and Fernandes, R. L., Integrability of Poisson brackets, J. Differential Geom. 66 (2004), 71–137.Google Scholar
Dixmier, J., Enveloping algebras, Graduate Studies in Mathematics, vol. 11 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Duistermaat, J. J. and Kolk, J., Lie groups, Universitext (Springer, Berlin, 2000).CrossRefGoogle Scholar
Knapp, A. W., Lie groups beyond an introduction, Progress in Mathematics, vol. 140, second edition (Birkhäuser, Boston, MA, 2002).Google Scholar
Mackenzie, K., General theory of Lie groupoids and Lie algebroids, London Mathematical Society Lecture Note Series, vol. 213 (Cambridge University Press, Cambridge, 2005).Google Scholar
Mărcuț, I., Rigidity around Poisson submanifolds, Acta Math., to appear, Preprint (2012),arXiv:1208.2297 [math.DG].Google Scholar
Mărcuț, I., Normal forms in Poisson geometry, PhD thesis, Utrecht University (2013),arXiv:1301.4571 [math.DG].Google Scholar
Papadima, S., Rigidity properties of compact Lie groups modulo maximal tori, Math. Ann. 275 (1986), 637–652.Google Scholar
Radko, O., A classification of topologically stable Poisson structures on a compact oriented surface, J. Symplectic Geom. 1 (2002), 523–542.Google Scholar
Schwarz, G. W., Smooth functions invariant under the action of a compact Lie group, Topology 14 (1975), 63–68.Google Scholar