Hostname: page-component-55f67697df-xq6d9 Total loading time: 0 Render date: 2025-05-09T05:53:17.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic base change of cuspidal automorphic representations over function fields

Part of: Discontinuous groups and automorphic forms Algebraic number theory: global fields Classical Topics in Algebraic Topology Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  11 September 2024

Gebhard Böckle Open the ORCID record for Gebhard Böckle [Opens in a new window] ,
Tony Feng Open the ORCID record for Tony Feng [Opens in a new window] ,
Michael Harris Open the ORCID record for Michael Harris [Opens in a new window] ,
Chandrashekhar B. Khare Open the ORCID record for Chandrashekhar B. Khare [Opens in a new window]  and
Jack A. Thorne Open the ORCID record for Jack A. Thorne [Opens in a new window]
Gebhard Böckle
Affiliation:
Interdisciplinary Center for Scientific Computing, Universität Heidelberg, 69120 Heidelberg, Germany [email protected]
Tony Feng
Affiliation:
Department of Mathematics, University of California at Berkeley, Berkeley, CA 94720, USA [email protected]
Michael Harris
Affiliation:
Department of Mathematics, Columbia University, New York, NY 10027, USA [email protected]
Chandrashekhar B. Khare
Affiliation:
Department of Mathematics, UCLA, Los Angeles, USA [email protected]
Jack A. Thorne
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Wilberforce Road, Cambridge, UK [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 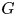$G$ be a split semisimple group over a global function field 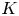$K$. Given a cuspidal automorphic representation 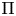$\Pi$ of 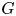$G$ satisfying a technical hypothesis, we prove that for almost all primes 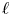$\ell$, there is a cyclic base change lifting of 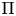$\Pi$ along any 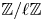$\mathbb {Z}/\ell \mathbb {Z}$-extension of 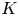$K$. Our proof does not rely on any trace formulas; instead it is based on using modularity lifting theorems, together with a Smith theory argument, to obtain base change for residual representations. As an application, we also prove that for any split semisimple group 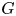$G$ over a local function field 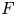$F$, and almost all primes 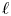$\ell$, any irreducible admissible representation of 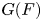$G(F)$ admits a base change along any 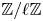$\mathbb {Z}/\ell \mathbb {Z}$-extension of 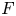$F$. Finally, we characterize local base change more explicitly for a class of toral representations considered in work of Chan and Oi.

Keywords

base changeSmith theorymodularity liftingfunction fields

MSC classification

Primary: 55M35: Finite groups of transformations (including Smith theory)
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11R39: Langlands-Weil conjectures, nonabelian class field theory 11S37: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 9 , September 2024 , pp. 1959 - 2004
Check for updates
Copyright
© The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Achar, P., Perverse sheaves and applications to representation theory, Mathematical Surveys and Monographs, vol. 258 (American Mathematical Society, Providence, RI, 2021).CrossRefGoogle Scholar
Arias-de Reyna, S. and Böckle, G., Deformation rings and images of Galois representations, Preprint, arXiv:2107.03114.Google Scholar
Arthur, J. and Clozel, L., Simple algebras, base change, and the advanced theory of the trace formula, Annals of Mathematics Studies, vol. 120 (Princeton University Press, Princeton, NJ, 1989).CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609.CrossRefGoogle Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers (French) [Perverse sheaves], in Analysis and topology on singular spaces, vol. I (Luminy, 1981), Astérisque, vol. 100 (Société Mathématique de France, Paris, 1982), 5–171.Google Scholar
Böckle, G., Gajda, W. and Petersen, S., On the semisimplicity of reductions and adelic openness for $E$-rational compatible systems over global function fields, Trans. Amer. Math. Soc. 372 (2019), 5621–5691.CrossRefGoogle Scholar
Böckle, G., Harris, M., Khare, C. and Thorne, J., ${\widehat {G}}$-local systems on smooth projective curves are potentially automorphic, Acta Math. 223 (2019), 1–111.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras, Elements of Mathematics (Berlin) (Springer, Berlin, 2005), ch. 7–9. Translated from the 1975 and 1982 French originals by Andrew Pressley.Google Scholar
Broué, M., Isométries de caractères et équivalences de Morita ou dérivées (French) [Isometries of characters and Morita or derived equivalences], Inst. Hautes Études Sci. Publ. Math. 71 (1990), 45–63.CrossRefGoogle Scholar
Cadoret, A. and Zheng, W., Ultraproduct coefficients in étale cohomology and torsion-freeness in compatible families, in preparation.Google Scholar
Česnavicius, K., Poitou–Tate without restrictions on the order, Math. Res. Lett. 22 (2015), 1621–1666.CrossRefGoogle Scholar
Chan, C. and Ivanov, A., Cohomological representations of parahoric subgroups, Represent. Theory 25 (2021), 1–26.CrossRefGoogle Scholar
Chan, C. and Oi, M., Geometric $L$-packets of Howe-unramified toral supercuspidal representations, J. Eur. Math. Soc. (2023), doi:10.4171/JEMS/1396.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$ Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.CrossRefGoogle Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.CrossRefGoogle Scholar
de Jong, A. J., A conjecture on arithmetic fundamental groups, Israel J. Math. 121 (2001), 61–84.CrossRefGoogle Scholar
Deligne, P., La conjecture de Weil. II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Deligne, P. and Lusztig, G., Representations of reductive groups over finite fields, Ann. of Math. (2) 103 (1976), 103–161.CrossRefGoogle Scholar
Drinfeld, V., On the pro-semisimple completion of the fundamental group of a smooth variety over a finite field, Adv. Math. 327 (2018), 708–788.CrossRefGoogle Scholar
Feit, W. and Seitz, G. M., On finite rational groups and related topics, Illinois J. Math. 33 (1989), 103–131.CrossRefGoogle Scholar
Feng, T., Smith theory and cyclic base change functoriality, Forum Math. Pi 12 (2024), 1–66.CrossRefGoogle Scholar
Fintzen, J., Tame cuspidal representations in non-defining characteristics, Michigan Math. J. 72 (2022), 331–342.CrossRefGoogle Scholar
Gaitsgory, D., On de Jong's conjecture, Israel J. Math. 157 (2007), 155–191.CrossRefGoogle Scholar
Gan, W. T., Harris, M. and Sawin, W., Local parameters of supercuspidal representations (with an appendix by Raphaël Beuzart-Plessis), Forum Math. Pi, to appear. Preprint (2021), arXiv:2109.07737.Google Scholar
Genestier, A. and Lafforgue, V., Chtoucas restreints pour les groupes réductifs et paramétrisation de Langlands locale, Preprint (2017), arXiv:1709.00978.Google Scholar
Gross, B. H. and Reeder, M., Arithmetic invariants of discrete Langlands parameters, Duke Math. J. 154 (2010), 431–508.CrossRefGoogle Scholar
Guiraud, D.-A., Unobstructedness of Galois deformation rings associated to regular algebraic conjugate self-dual cuspidal automorphic representations, Algebra Number Theory 14 (2020), 1331–1380.CrossRefGoogle Scholar
Harder, G., Chevalley groups over function fields and automorphic forms, Ann. of Math. (2) 100 (1974), 249–306.CrossRefGoogle Scholar
Heinloth, J., Ngô, B.-C. and Yun, Z., Kloosterman sheaves for reductive groups, Ann. of Math. (2) 177 (2013), 241–310.CrossRefGoogle Scholar
Hiss, G., Die adjungierten Darstellungen der Chevalley-Gruppen, Arch. Math. (Basel) 42 (1984), 408–416.CrossRefGoogle Scholar
Hogeweij, G. M. D., Almost-classical Lie algebras. I, II, Nederl. Akad. Wetensch. Indag. Math. 44 (1982), 441–452, 453–460.CrossRefGoogle Scholar
Ito, K., On a torsion analogue of the weight-monodromy conjecture, Doc. Math. 26 (2021), 1729–1770.CrossRefGoogle Scholar
Kaletha, T., Regular supercuspidal representations, J. Amer. Math. Soc. 32 (2019), 1071–1170.CrossRefGoogle Scholar
Khare, C. and Thorne, J. A., Potential automorphy and the Leopoldt conjecture, Amer. J. Math. 139 (2017), 1205–1273.CrossRefGoogle Scholar
Khare, C. and Wintenberger, J.-P., Serre's modularity conjecture. II, Invent. Math. 178 (2009), 505–586.CrossRefGoogle Scholar
Labesse, J.-P., Cohomologie, stabilisation et changement de base, Astérisque 257 (1999).Google Scholar
Labesse, J.-P. and Lemaire, B., La formule des traces tordue pour les corps de fonctions, Preprint (2021), arXiv:2102.02517.Google Scholar
Lafforgue, L., Chtoucas de Drinfeld et correspondance de Langlands, Invent. Math. 147 (2002), 1–241.CrossRefGoogle Scholar
Lafforgue, V., Chtoucas pour les groupes réductifs et paramétrisation de Langlands globale, J. Amer. Math. Soc. 31 (2018), 719–891.CrossRefGoogle Scholar
Larsen, M., Maximality of Galois actions for compatible systems, Duke Math. J. 80 (1995), 601–630.CrossRefGoogle Scholar
Laumon, G., Cohomology of Drinfeld modular varieties. Part I. Geometry, counting of points and local harmonic analysis (Cambridge University Press, Cambridge, 1996).Google Scholar
Malle, G. and Testerman, D., Linear algebraic groups and finite groups of Lie type (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Patrikis, S., Deformations of Galois representations and exceptional monodromy, Invent. Math. 205 (2016), 269–336.CrossRefGoogle Scholar
Ronchetti, N., Local base change via Tate cohomology, Represent. Theory 20 (2016), 263–294.CrossRefGoogle Scholar
Sawin, W. and Templier, N., On the Ramanujan conjecture for automorphic forms over function fields I. Geometry, J. Amer. Math. Soc. 34 (2021), 653–746.CrossRefGoogle Scholar
Saxl, J. and Seitz, G. M., Subgroups of algebraic groups containing regular unipotent elements, J. Lond. Math. Soc. (2) 55 (1997), 370–386.CrossRefGoogle Scholar
Seitz, G. M., The root subgroups for maximal tori in finite groups of Lie type, Pacific J. Math. 106 (1983), 153–244.CrossRefGoogle Scholar
Springer, T. A. and Steinberg, R., Conjugacy classes, in Seminar on algebraic groups and related finite groups (The Institute for Advanced Study, Princeton, NJ, 1968/69), Lecture Notes in Mathematics, vol. 131 (Springer, Berlin, 1970), 167–266.CrossRefGoogle Scholar
Treumann, D. and Venkatesh, A., Functoriality, Smith theory, and the Brauer homomorphism, Ann. of Math. (2) 183 (2016), 177–228.CrossRefGoogle Scholar
Varshavsky, Y., Moduli spaces of principal $F$-bundles, Selecta Math. (N.S.) 10 (2004), 131–166.CrossRefGoogle Scholar
Vignéras, M.-F., Représentations $\ell$-modulaires d'un groupe réductif $p$-adique avec $\ell \neq p$, Progress in Mathematics, vol. 137 (Birkhäuser, Boston, 1996).Google Scholar
Vignéras, M.-F., Irreducible modular representations of a reductive p-adic group and simple modules for Hecke algebras, in European Congress of Mathematics, vol. I (Barcelona, 2000), Progress in Mathematics, vol. 201 (Birkhäuser, Basel, 2001), 117–133.Google Scholar
Völklein, H., The $1$-cohomology of the adjoint module of a Chevalley group, Forum Math. 1 (1989), 1–13.CrossRefGoogle Scholar
Xue, C., Finiteness of cohomology groups of stacks of shtukas as modules over Hecke algebras, and applications, Épijournal Géom. Algébrique 4 (2020), 1–42, Art. 6.Google Scholar
Xue, C., Cohomology with integral coefficients of stacks of shtukas, Preprint (2020), arXiv:2001.05805.Google Scholar
Yao, Z., The Breuil–Mézard conjecture for function fields, Preprint, arXiv:1808.09433.Google Scholar
Yun, Z., Epipelagic representations and rigid local systems, Selecta Math. (N.S.) 22 (2016), 1195–1243.CrossRefGoogle Scholar