Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-21T19:53:41.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Cusp eigenforms and the hall algebra of an elliptic curve

Part of: Lie algebras and Lie superalgebras Discontinuous groups and automorphic forms Lie groups Algebraic number theory: global fields

Published online by Cambridge University Press:  04 March 2013

Dragos Fratila
Dragos Fratila*
Affiliation:
Université Paris Denis-Diderot - Paris 7, Institut de Mathématiques de Jussieu, UMR 7586 du CNRS, Batiment Chevaleret, 75205 Paris Cedex 13, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an explicit construction of the cusp eigenforms on an elliptic curve defined over a finite field, using the theory of Hall algebras and the Langlands correspondence for function fields and 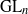${\mathrm{GL} }_{n} $. As a consequence we obtain a description of the Hall algebra of an elliptic curve as an infinite tensor product of simpler algebras. We prove that all these algebras are specializations of a universal spherical Hall algebra (as defined and studied by Burban and Schiffmann  [On the Hall algebra of an elliptic curve I, Preprint (2005), arXiv:math/0505148 [math.AG]] and Schiffmann and Vasserot [The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials, Compositio Math. 147 (2011), 188–234]).

Keywords

Hall algebraselliptic curvesautomorphic forms

MSC classification

Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11R39: Langlands-Weil conjectures, nonabelian class field theory 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings 17B99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 6 , June 2013 , pp. 914 - 958
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, E. and Tate, J., Class field theory, Advanced Book Classics, second edition (Addison-Wesley, Redwood City, CA, 1990).Google Scholar
Atiyah, M., Vector bundles on elliptic curves, Proc. Lond. Math. Soc (3) 7 (1957), 414–452.Google Scholar
Baumann, P. and Kassel, C., The Hall algebra of coherent sheaves on the projective line, J. Reine Angew. Math. 533 (2001), 207–233.Google Scholar
Burban, I. and Schiffmann, O., On the Hall algebra of an elliptic curve I, Preprint (2005), arXiv:math/0505148 [math.AG].Google Scholar
Cassels, J. W. S. and Fröhlich, A.(eds), Algebraic number theory (Thompson, Washington, DC, 1976).Google Scholar
Cramer, T., Double Hall algebras and derived equivalences, Adv. Math. 224 (2010), 1097–1120.CrossRefGoogle Scholar
Drinfel’d, V., Langlands conjecture for $\mathrm{GL} (2)$ over function fields, in Proc. int. cong. math., Helsinki, 1978 (Acad. Sci. Fennica, Helsinki, 1980), 565–574.Google Scholar
Frenkel, E., Lectures on the Langlands program and conformal field theory, Preprint (2005), arXiv:hep-th/0512172.Google Scholar
Green, J., Hall algebras, hereditary algebras and quantum groups, Invent. Math. 120 (1995), 361–377.Google Scholar
Grothendieck, A., Sur la classification des fibrés holomorphes sur la sphère de Riemann, Amer. J. Math. 79 (1957), 121–138.CrossRefGoogle Scholar
Harder, G., Minkowskische Reduktionstheorie ber Funktionenkrpern., Invent. Math. 7 (1969), 33–54.CrossRefGoogle Scholar
Harder, G., Chevalley groups over function fields and Autormorphic forms, Ann. of Math. (2) 100 (1974), 249–306.CrossRefGoogle Scholar
Harder, G. and Narasimhan, M. S., On the cohomology groups of moduli of vector bundles on curves, Math. Ann. 212 (1975), 215–248.Google Scholar
Jacquet, H., Piatetski-Shapiro, I. I. and Shalika, J., Rankin–Selberg convolutions, Amer. J. Math. 105 (1983), 367–464.Google Scholar
Joseph, A., Quantum groups and their primitive ideals, Ergeb. Math. Grenzgeb. (3), Vol. 29 (Springer, Berlin, 1995).CrossRefGoogle Scholar
Kapranov, M., Eisenstein series and quantum affine algebras, J. Math. Sci. (N. Y.) 84 (1997), 1311–1360.CrossRefGoogle Scholar
Kapranov, M., Schiffmann, O. and Vasserot, E., Hall algebras of curves as shuffle algebras, Preprint (2011).Google Scholar
Kassel, C., Rosso, M. and Turaev, V., Quantum groups and knot invariants (Société mathématique de France, 1997).Google Scholar
Kuleshov, S. A., Construction of bundles on an elliptic curve, in Helices and vector bundles, Séminaire Rudakov, London Mathematical Society Lecture Note Series, vol. 148 (Cambridge University Press, Cambridge, 1990), 7–22.CrossRefGoogle Scholar
Lafforgue, L., Chtoukas de Drinfel’d et correspondance de Langlands, Invent. Math. 147 (2002), 1–241.Google Scholar
Laumon, G., Faisceaux automorphes liés aux séries d’Eisenstein, in Automorphic forms, Shimura varieties, and L-functions (Ann Arbor, MI, 1988), Vol I, Perspectives in Mathematics, vol. 10 (Academic Press, Boston, MA, 1990), 227–281.Google Scholar
Lenzing, H. and Meltzer, H., Sheaves on a weighted projective line of genus one, and represen- tations of a tubular algebra, in Representations of algebras (Ottawa, 1992), CMS Conference Proceedings, vol. 14 (American Mathematical Society, Providence, RI, 1994), 313–337.Google Scholar
Macdonald, I., Symmetric functions and Hall polynomials, Oxford Mathematical Monographs, second edition (The Clarendon Press, Oxford, 1995).CrossRefGoogle Scholar
Piatetski-Shapiro, I. I., Multiplicity one theorems, in Automorphic forms, representations and L-functions (Proc. Symp. Pure Math., Oregon State Univ., Corvallis, OR, 1977), Part 1, Proc. Sympos. Pure Math., vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 209–212.Google Scholar
Ringel, C., Hall algebras and quantum groups, Invent. Math. 101 (1990), 583–591.CrossRefGoogle Scholar
Schiffmann, O., Noncommutative projective curves and quantum loop algebras, Duke Math. J. 121 (2004), 113–168.CrossRefGoogle Scholar
Schiffmann, O., Lectures on Hall algebras, Preprint (2009), arXiv:math/0611617v2 [math.RT].Google Scholar
Schiffmann, O., Drinfeld realization of the elliptic Hall algebra, J. Algebraic Combin. 35 (2012), 237–262.Google Scholar
Schiffmann, O., On the Hall algebra of an elliptic curve II, Duke Math. J. 161 (2012), 1711–1750.Google Scholar
Schiffmann, O. and Vasserot, E., The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials, Compositio Math. 147 (2011), 188–234.Google Scholar
Schiffmann, O. and Vasserot, E., Hall algebras of curves, commuting varieties and Langlands duality, Math. Ann. 353 (2012), 1399–1451.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E., The elliptic Hall algebra and the $K$-theory of the Hilbert scheme of ${ \mathbb{A} }^{2} $, Preprint (2012), arXiv:0905.2555v3 [math.QA].Google Scholar
Seidel, R. T., Braid group actions on derived categories of coherent sheaves, Duke Math. J. 108 (2001), 37–108.Google Scholar
Serre, J.  P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, 1977).CrossRefGoogle Scholar
Shalika, J., The multiplicity one theorem for $GL(n)$, Ann. of Math. (2) 100, (1974), 171–193.Google Scholar