Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T12:35:21.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting fundamental solutions to the Pell equation with prescribed size

Part of: Multiplicative number theory Finite fields and commutative rings (number-theoretic aspects) Exponential sums and character sums Diophantine equations

Published online by Cambridge University Press:  11 October 2018

Ping Xi
Ping Xi*
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The cardinality of the set of 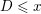$D\leqslant x$ for which the fundamental solution of the Pell equation 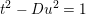$t^{2}-Du^{2}=1$ is less than 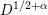$D^{1/2+\unicode[STIX]{x1D6FC}}$ with 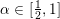$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$ is studied and certain lower bounds are obtained, improving previous results of Fouvry by introducing the 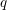$q$-analogue of van der Corput method to algebraic exponential sums with smooth moduli.

Keywords

Pell equationexponential sumsq-analogue of van der Corput method

MSC classification

Primary: 11D09: Quadratic and bilinear equations 11N37: Asymptotic results on arithmetic functions 11L07: Estimates on exponential sums 11T23: Exponential sums
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 11 , November 2018 , pp. 2379 - 2402
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bombieri, E., On exponential sums in finite fields , Amer. J. Math. 88 (1966), 71–105.Google Scholar
Bourgain, J., A remark on solutions of the Pell equation , Int. Math. Res. Not. IMRN 2015 (2015), 2841–2855.Google Scholar
Fouvry, É., On the size of the fundamental solution of the Pell equation , J. Reine Angew. Math. 717 (2016), 1–33.Google Scholar
Fouvry, É. and Jouve, F., Fundamental solutions to Pell equation with prescribed size , Proc. Steklov Inst. Math. 276 (2012), 40–50.Google Scholar
Heath-Brown, D. R., Hybrid bounds for Dirichlet L-functions , Invent. Math. 47 (1978), 149–170.Google Scholar
Heath-Brown, D. R., A mean value estimate for real character sums , Acta Arith. 72 (1995), 235–275.Google Scholar
Hooley, C., On the Pellian equation and the class number of indefinite binary quadratic forms , J. Reine Angew. Math. 353 (1984), 98–131.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory, Cambridge Studies in Advanced Mathematics, vol. 46 (Cambridge University Press, Cambridge, 1995).Google Scholar
Tenenbaum, G. and Wu, J., Moyennes de certaines fonctions multiplicatives sur les entiers friables , J. Reine Angew. Math. 564 (2003), 119–166.Google Scholar
Weil, A., On some exponential sums , Proc. Natl. Acad. Sci. USA 34 (1948), 204–207.Google Scholar
Wu, J. and Xi, P., Arithmetic exponent pairs for algebraic trace functions and applications, Preprint (2016), arXiv:1603.07060 [math.NT].Google Scholar