Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-24T16:53:37.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Completed prismatic F-crystals and crystalline Zp-local systems

Part of: Discontinuous groups and automorphic forms (Co)homology theory

Published online by Cambridge University Press:  18 April 2024

Heng Du Open the ORCID record for Heng Du [Opens in a new window] ,
Tong Liu ,
Yong Suk Moon Open the ORCID record for Yong Suk Moon [Opens in a new window]  and
Koji Shimizu Open the ORCID record for Koji Shimizu [Opens in a new window]
Heng Du
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, PR China [email protected]
Tong Liu
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907, USA [email protected]
Yong Suk Moon
Affiliation:
Beijing Institute of Mathematical Sciences and Applications, Beijing 101408, PR China [email protected]
Koji Shimizu
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, PR China [email protected] and Beijing Institute of Mathematical Sciences and Applications, Beijing 101408, PR China
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of completed 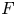$F$-crystals on the absolute prismatic site of a smooth 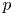$p$-adic formal scheme. We define a functor from the category of completed prismatic 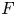$F$-crystals to that of crystalline étale 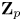$\mathbf {Z}_p$-local systems on the generic fiber of the formal scheme and show that it gives an equivalence of categories. This generalizes the work of Bhatt and Scholze, which treats the case of a mixed characteristic complete discrete valuation ring with perfect residue field.

Keywords

p-adic Hodge theorycrystalline local systemsprismatic F-crystals

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology
Secondary: 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 5 , May 2024 , pp. 1101 - 1166
Check for updates
Copyright
© 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The third and fourth authors are partially supported by an AMS–Simons Travel Grant.

References

Andreatta, F., Generalized ring of norms and generalized $(\varphi, \Gamma )$-modules, Ann. Sci. Éc. Norm. Supér. (4) 39 (2006), 599–647.CrossRefGoogle Scholar
Anschütz, J. and Le Bras, A.-C., Prismatic Dieudonné theory, Forum Math. Pi 11 (2023), e2; MR4530092.CrossRefGoogle Scholar
Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné cristalline II, Lecture Notes in Mathematics, vol. 930 (Springer, Berlin, New York, Heidelberg, 1982).CrossRefGoogle Scholar
Bhatt, B., Algebraic geometry in mixed characteristic, Preprint (2021), arXiv:2112.12010.Google Scholar
Bhatt, B. and Lurie, J., Absolute prismatic cohomology, Preprint (2022), arXiv:2201.06120.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral $p$-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Topological Hochschild homology and integral $p$-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 129 (2019), 199–310.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., The pro-étale topology for schemes, Astérisque 369 (2015), 99–201; MR3379634.Google Scholar
Bhatt, B. and Scholze, P., Prisms and prismatic cohomology, Preprint (2021), arXiv:1905.08229v3.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., Prisms and prismatic cohomology, Ann. of Math. (2) 196 (2022), 1135–1275.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., Prismatic $F$-crystals and crystalline Galois representations, Camb. J. Math. 11 (2023), 507–562; MR4600546.CrossRefGoogle Scholar
Breuil, C., Représentations $p$-adiques semi-stables et transversalité de Griffiths, Math. Ann. 307 (1997), 191–224.CrossRefGoogle Scholar
Brinon, O., Représentations cristallines dans le cas d'un corps résiduel imparfait, Ann. Inst. Fourier (Grenoble) 56 (2006), 919–999; MR2266883.CrossRefGoogle Scholar
Brinon, O., Représentations $p$-adiques cristallines et de de Rham dans le cas relatif, Mém. Soc. Math. Fr. 112 (2008).Google Scholar
Brinon, O. and Trihan, F., Représentations cristallines et $F$-cristaux: le cas d'un corps résiduel imparfait, Rend. Semin. Mat. Univ. Padova 119 (2008), 141–171.CrossRefGoogle Scholar
Colmez, P. and Fontaine, J.-M., Construction des représentations $p$-adiques semi-stables, Invent. Math. 140 (2000), 1–43.CrossRefGoogle Scholar
De Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96.CrossRefGoogle Scholar
Drinfeld, V., A stacky approach to crystals, in Dialogues between physics and mathematics: C. N. Yang at 100 (Springer, Cham, 2022), 19–47.Google Scholar
Du, H. and Liu, T., A prismatic approach to $(\varphi, \hat {G})$-modules and $F$-crystals, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2023), arXiv:2107.12240v3.Google Scholar
Faltings, G., Crystalline cohomology and p-adic Galois representations, in Algebraic analysis, geometry, and number theory (Johns Hopkins University Press, Baltimore, 1988), 25–80.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux (1ère partie) (Birkhäuser, Boston, MA, 2007), 249–309.Google Scholar
Gabber, O. and Ramero, L., Almost ring theory, Lecture Notes in Mathematics, vol. 1800 (Springer, Berlin, 2003).CrossRefGoogle Scholar
Gao, H., Integral $p$-adic Hodge theory in the imperfect residue field case, Preprint (2020), arXiv:2007.06879v2.Google Scholar
Gao, H. and Liu, T., Loose crystalline lifts and overconvergence of étale $(\varphi, \tau )$-modules, Amer. J. Math. 142 (2020), 1733–1770.CrossRefGoogle Scholar
Guo, H. and Reinecke, E., A prismatic approach to crystalline local systems, Preprint (2022), arXiv:2203.09490v2.Google Scholar
Horrocks, G., Vector bundles on the punctured spectrum of a local ring, Proc. Lond. Math. Soc. (3) 14 (1964), 689–713; MR169877.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, E30 (Friedrich Vieweg & Sohn, Braunschweig, 1996); MR1734903.CrossRefGoogle Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, in Modular functions of one variable, III (Proceedings International Summer School, University of Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, vol. 350 (Springer, Berlin, 1973), 69–190; MR447119.Google Scholar
Kedlaya, K. and Liu, R., Relative $p$-adic Hodge theory: foundations, Astérisque 371 (2015), 239.Google Scholar
Kim, W., The relative Breuil-Kisin classification of $p$-divisible groups and finite flat group schemes, Int. Math. Res. Not. IMRN 2015 (2015), 8152–8232.CrossRefGoogle Scholar
Kisin, M., Crystalline representations and F-crystals, in Algebraic geometry and number theory, Progress in Mathematics, vol. 253 (Birkhäuser, Boston, 2006), 459–496.CrossRefGoogle Scholar
Kisin, M., Integral models for Shimura varieties of abelian type, J. Amer. Math. Soc. 23 (2010), 967–1012; MR2669706 (2011j:11109).CrossRefGoogle Scholar
Kurano, K. and Shimomoto, K., Ideal-adic completion of quasi-excellent rings (after Gabber), Kyoto J. Math. 61 (2021), 707–722; MR4301055.CrossRefGoogle Scholar
Li, S. and Liu, T., Comparison of prismatic cohomology and derived de Rham cohomology, J. Eur. Math. Soc. (JEMS) (2023), doi:10.4171/JEMS/1377.CrossRefGoogle Scholar
Liu, T., Torsion $p$-adic Galois representations and a conjecture of Fontaine, Ann. Sci. Éc. Norm. Supér. 40 (2007), 633–674.CrossRefGoogle Scholar
Liu, T., On lattices in semi-stable representations: a proof of a conjecture of Breuil, Compos. Math. 144 (2008), 61–88.CrossRefGoogle Scholar
Liu, T. and Moon, Y. S., Relative crystalline representations and $p$-divisible groups in the small ramification case, Algebra Number Theory 14 (2020), 2773–2789.CrossRefGoogle Scholar
Martin, F., Analytic functions on tubes of nonarchimedean analytic spaces, Algebra Number Theory 11 (2017), 657–683, with an appendix by Kappen and Martin; MR3649364.CrossRefGoogle Scholar
Mathew, A., Faithfully flat descent of almost perfect complexes in rigid geometry, J. Pure Appl. Algebra 226 (2022), 106938.CrossRefGoogle Scholar
Min, Y. and Wang, Y., Relative $(\varphi, \Gamma )$-modules and prismatic $F$-crystals, Preprint (2021), arXiv:2110.06076v2.Google Scholar
Moon, Y. S., Strongly divisible lattices and crystalline cohomology in the imperfect residue field case, Selecta Math. (N.S.), to appear. Preprint (2023), arXiv:2110.06001v4.CrossRefGoogle Scholar
Morrow, M. and Tsuji, T., Generalised representations as q-connections in integral $p$-adic Hodge theory, Preprint (2021), arXiv:2010.04059v2.Google Scholar
Ogus, A., F-isocrystals and de Rham cohomology. II – Convergent isocrystals, Duke Math. J. 51 (1984), 765–850.CrossRefGoogle Scholar
Ohkubo, S., The $p$-adic monodromy theorem in the imperfect residue field case, Algebra Number Theory 7 (2013), 1977–2037; MR3134041.CrossRefGoogle Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.CrossRefGoogle Scholar
Scholze, P., $p$-adic Hodge theory for rigid-analytic varieties, Forum Math. Pi 1 (2013), e1.CrossRefGoogle Scholar
Scholze, P., $p$-adic Hodge theory for rigid-analytic varieties—corrigendum, Forum Math. Pi 4 (2016), e6; MR3535697.CrossRefGoogle Scholar
The Stacks Project Authors, The stacks project (2022), https://stacks.math.columbia.edu.Google Scholar
Tan, F. and Tong, J., Crystalline comparison isomorphisms in $p$-adic Hodge theory: the absolutely unramified case, Algebra Number Theory 13 (2019), 1509–1581; MR4009670.Google Scholar
Tate, J., p-divisible groups, in Proceedings of a conference on local fields (Springer, Berlin, Heidelberg, 1967), 158–183.CrossRefGoogle Scholar
Tian, Y., Finiteness and duality for the cohomology of prismatic crystals, J. Reine Angew. Math. 800 (2023), 217–257; MR4609829.Google Scholar
Vasiu, A. and Zink, T., Purity results for $p$-divisible groups and abelian schemes over regular bases of mixed characteristic, Doc. Math. 15 (2010), 571–599.CrossRefGoogle Scholar
Wu, Z., Galois representations, $(\varphi, \Gamma )$-modules and prismatic F-crystals, Doc. Math. 26 (2021), 1771–1798.CrossRefGoogle Scholar
Yekutieli, A., Flatness and completion revisited, Algebr. Represent. Theory 21 (2018), 717–736.CrossRefGoogle Scholar