Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T15:53:39.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding the covolume of lattices in products

Part of: Lie groups Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  11 October 2019

Pierre-Emmanuel Caprace  and
Adrien Le Boudec
Pierre-Emmanuel Caprace
Affiliation:
UCLouvain, 1348 Louvain-la-Neuve, Belgium email [email protected]
Adrien Le Boudec
Affiliation:
UMPA – ENS Lyon, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study lattices in a product 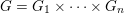$G=G_{1}\times \cdots \times G_{n}$ of non-discrete, compactly generated, totally disconnected locally compact (tdlc) groups. We assume that each factor is quasi just-non-compact, meaning that 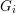$G_{i}$ is non-compact and every closed normal subgroup of 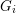$G_{i}$ is discrete or cocompact (e.g. 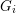$G_{i}$ is topologically simple). We show that the set of discrete subgroups of 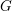$G$ containing a fixed cocompact lattice 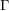$\unicode[STIX]{x1D6E4}$ with dense projections is finite. The same result holds if 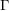$\unicode[STIX]{x1D6E4}$ is non-uniform, provided 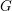$G$ has Kazhdan’s property (T). We show that for any compact subset 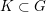$K\subset G$, the collection of discrete subgroups 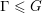$\unicode[STIX]{x1D6E4}\leqslant G$ with 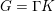$G=\unicode[STIX]{x1D6E4}K$ and dense projections is uniformly discrete and hence of covolume bounded away from 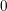$0$. When the ambient group 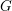$G$ is compactly presented, we show in addition that the collection of those lattices falls into finitely many 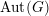$\operatorname{Aut}(G)$-orbits. As an application, we establish finiteness results for discrete groups acting on products of locally finite graphs with semiprimitive local action on each factor. We also present several intermediate results of independent interest. Notably it is shown that if a non-discrete, compactly generated quasi just-non-compact tdlc group 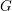$G$ is a Chabauty limit of discrete subgroups, then some compact open subgroup of 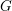$G$ is an infinitely generated pro-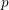$p$ group for some prime 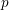$p$. It is also shown that in any Kazhdan group with discrete amenable radical, the lattices form an open subset of the Chabauty space of closed subgroups.

MSC classification

Primary: 20E08: Groups acting on trees 20E32: Simple groups 22D05: General properties and structure of locally compact groups 22E40: Discrete subgroups of Lie groups
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 12 , December 2019 , pp. 2296 - 2333
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is an F.R.S.-FNRS Senior Research Associate. The second author is a CNRS Researcher. This work was partially carried out when the second author was an F.R.S.-FNRS Post-Doctoral Researcher at UCLouvain. This work was partially supported by ANR-14-CE25-0004 GAMME.

References

Aschbacher, M., Finite group theory, Cambridge Studies in Advanced Mathematics, vol. 10, second edition (Cambridge University Press, Cambridge, 2000).Google Scholar
Bader, U., Duchesne, B. and Lécureux, J., Amenable invariant random subgroups , Israel J. Math. 213 (2016), 399–422; with an appendix by Phillip Wesolek.Google Scholar
Bader, U., Furman, A. and Sauer, R., An adelic arithmeticity theorem for lattices in products , Math. Z. (2019), doi:10.1007/s00209-019-02241-9.Google Scholar
Bader, U. and Shalom, Y., Factor and normal subgroup theorems for lattices in products of groups , Invent. Math. 163 (2006), 415–454.Google Scholar
Barnea, Y., Ershov, M. and Weigel, T., Abstract commensurators of profinite groups , Trans. Amer. Math. Soc. 363 (2011), 5381–5417.Google Scholar
Bass, H. and Kulkarni, R., Uniform tree lattices , J. Amer. Math. Soc. 3 (1990), 843–902.Google Scholar
Bass, H. and Lubotzky, A., Tree lattices, Progress in Mathematics, vol. 176 (Birkhäuser, Boston, MA, 2001), with appendices by Bass, L. Carbone, Lubotzky, G. Rosenberg and J. Tits.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan’s property (T), New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008).Google Scholar
Bourdon, M., Sur les immeubles fuchsiens et leur type de quasi-isométrie , Ergodic Theory Dynam. Systems 20 (2000), 343–364.Google Scholar
Burger, M. and Mozes, S., Groups acting on trees: from local to global structure , Publ. Math. Inst. Hautes Études Sci. 2001 (2000), 113–150.Google Scholar
Burger, M. and Mozes, S., Lattices in product of trees , Publ. Math. Inst. Hautes Études Sci. 2001 (2000), 151–194.Google Scholar
Burger, M. and Mozes, S., Lattices in products of trees and a theorem of H. C. Wang , Bull. Lond. Math. Soc. 46 (2014), 1126–1132.Google Scholar
Caprace, P.-E., Amenable groups and Hadamard spaces with a totally disconnected isometry group , Comment. Math. Helv. 84 (2009), 437–455.Google Scholar
Caprace, P.-E. and Monod, N., Isometry groups of non-positively curved spaces: discrete subgroups , J. Topol. 2 (2009), 701–746.Google Scholar
Caprace, P.-E. and Monod, N., Decomposing locally compact groups into simple pieces , Math. Proc. Cambridge Philos. Soc. 150 (2011), 97–128.Google Scholar
Caprace, P.-E. and Monod, N., A lattice in more than two Kac–Moody groups is arithmetic , Israel J. Math. 190 (2012), 413–444.Google Scholar
Caprace, P.-E. and Radu, N., Chabauty limits of simple groups acting on trees , J. Inst. Math. Jussieu (2019), doi:10.1017/S1474748018000348.Google Scholar
Caprace, P.-E., Reid, C. and Wesolek, P., Approximating simple locally compact groups by their dense locally compact subgroups , Int. Math. Res. Not. (2019), doi:10.1093/imrn/rny298.Google Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., Locally normal subgroups of totally disconnected groups. Part II: compactly generated simple groups , Forum Math. Sigma 5 (2017), e12.Google Scholar
Caprace, P.-E. and Wesolek, P., Indicability, residual finiteness, and simple subquotients of groups acting on trees , Geom. Topol. 22 (2018), 4163–4204.Google Scholar
Chabauty, C., Limite d’ensembles et géométrie des nombres , Bull. Soc. Math. France 78 (1950), 143–151.Google Scholar
Cornulier, Y., Commability and focal locally compact groups , Indiana Univ. Math. J. 64 (2015), 115–150.Google Scholar
Cornulier, Y. and de la Harpe, P., Metric geometry of locally compact groups, EMS Tracts in Mathematics, vol. 25 (European Mathematical Society (EMS), Zürich, 2016); winner of the 2016 EMS Monograph Award.Google Scholar
Dixon, J. D., du Sautoy, M. P. F., Mann, A. and Segal, D., Analytic pro-p-groups, London Mathematical Society Lecture Note Series, vol. 157 (Cambridge University Press, Cambridge, 1991).Google Scholar
Fell, J. M. G., Weak containment and induced representations of groups. II , Trans. Amer. Math. Soc. 110 (1964), 424–447.Google Scholar
Furman, A., On minimal strongly proximal actions of locally compact groups , Israel J. Math. 136 (2003), 173–187.Google Scholar
Furstenberg, H., Rigidity and cocycles for ergodic actions of semisimple Lie groups (after G. A. Margulis and R. Zimmer) , in Bourbaki Seminar, Vol. 1979/80, Lecture Notes in Mathematics, vol. 842 (Springer, Berlin–New York, 1981), 273–292.Google Scholar
Gartside, P. and Smith, M., Counting the closed subgroups of profinite groups , J. Group Theory 13 (2010), 41–61.Google Scholar
Gelander, T., Homotopy type and volume of locally symmetric manifolds , Duke Math. J. 124 (2004), 459–515.Google Scholar
Gelander, T., A lecture on invariant random subgroups , in New directions in locally compact groups, London Mathematical Society Lecture Note Series, vol. 447 (Cambridge University Press, 2018), 186–204.Google Scholar
Gelander, T. and Levit, A., Local rigidity of uniform lattices , Comment. Math. Helv. 93 (2018), 781–827.Google Scholar
Giudici, M. and Morgan, L., A theory of semiprimitive groups , J. Algebra 503 (2018), 146–185.Google Scholar
Glasner, Y., A two-dimensional version of the Goldschmidt–Sims conjecture , J. Algebra 269 (2003), 381–401.Google Scholar
Kakutani, S. and Kodaira, K., Über das Haarsche Mass in der lokal bikompakten Gruppe , Proc. Imp. Acad. Tokyo 20 (1944), 444–450.Google Scholar
Kazhdan, D. A. and Margulis, G. A., A proof of Selberg’s hypothesis , Mat. Sb. (N.S.) 75 (1968), 163–168.Google Scholar
Kuranishi, M., On everywhere dense imbedding of free groups in Lie groups , Nagoya Math. J. 2 (1951), 63–71.Google Scholar
Margulis, G. A., Discrete subgroups of semisimple Lie groups, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 17 (Springer, Berlin, 1991).Google Scholar
Morgan, L., Spiga, P. and Verret, G., On the order of Borel subgroups of group amalgams and an application to locally-transitive graphs , J. Algebra 434 (2015), 138–152.Google Scholar
Potočnik, P., Spiga, P. and Verret, G., On graph-restrictive permutation groups , J. Combin. Theory Ser. B 102 (2012), 820–831.Google Scholar
Praeger, C. E., Finite quasiprimitive group actions on graphs and designs , in Groups—Korea ’98 (Pusan) (de Gruyter, Berlin, 2000), 319–331.Google Scholar
Radu, N., A classification theorem for boundary 2-transitive automorphism groups of trees , Invent. Math. 209 (2017), 1–60.Google Scholar
Raghunathan, M. S., Discrete subgroups of Lie groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 68 (Springer, New York–Heidelberg, 1972).Google Scholar
Reid, C. D., Distal actions on coset spaces in totally disconnected, locally compact groups , J. Topol. Anal. (2018), to appear.Google Scholar
Shalom, Y., Rigidity of commensurators and irreducible lattices , Invent. Math. 141 (2000), 1–54.Google Scholar
Spiga, P., On G-locally primitive graphs of locally twisted wreath type and a conjecture of Weiss , J. Combin. Theory Ser. A 118 (2011), 2257–2260.Google Scholar
Spiga, P., An application of the local C (G, T) theorem to a conjecture of Weiss , Bull. Lond. Math. Soc. 48 (2016), 12–18.Google Scholar
Spiga, P. and Verret, G., On intransitive graph-restrictive permutation groups , J. Algebraic Combin. 40 (2014), 179–185.Google Scholar
Tits, J., Automorphismes à déplacement borné des groupes de Lie , Topology 3 (1964), 97–107.Google Scholar
Tits, J., Sur le groupe des automorphismes d’un arbre , in Essays on topology and related topics: Mémoires dédiés à Georges de Rham (Springer, New York, 1970), 188–211.Google Scholar
Tornier, S., Groups acting on trees and contributions to Willis theory, PhD thesis, ETH Zürich (2018).Google Scholar
Trofimov, V. I., Groups of automorphisms of graphs as topological groups , Mat. Zametki 38 (1985), 378–385, 476.Google Scholar
Trofimov, V. I. and Weiss, R. M., Graphs with a locally linear group of automorphisms , Math. Proc. Cambridge Philos. Soc. 118 (1995), 191–206.Google Scholar
Wang, H. C., On a maximality property of discrete subgroups with fundamental domain of finite measure , Amer. J. Math. 89 (1967), 124–132.Google Scholar
Wang, H. C., Topics on totally discontinuous groups , in Symmetric spaces, Pure and Applied Mathematics, vol. 8 (Dekker, New York, 1972), 459–487.Google Scholar
Wang, S. P., On isolated points in the dual spaces of locally compact groups , Math. Ann. 218 (1975), 19–34.Google Scholar
Weiss, R., An application of p-factorization methods to symmetric graphs , Math. Proc. Cambridge Philos. Soc. 85 (1979), 43–48.Google Scholar
Weiss, R., s-transitive graphs , in Algebraic methods in graph theory, Vols. I, II (Szeged 1978), Colloquia Mathematica Societatis János Bolyai, vol. 25 (North-Holland, Amsterdam–New York, 1981), 827–847.Google Scholar
Zassenhaus, H., Beweis eines Satzes über diskrete Gruppen , Abh. Math. Semin. Univ. Hambg. 12 (1938), 289–312.Google Scholar