Article contents
Bad reduction of genus 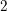 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
Published online by Cambridge University Press: 11 September 2017
Abstract
We show that a genus 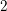 $2$ curve over a number field whose jacobian has complex multiplication will usually have stable bad reduction at some prime. We prove this by computing the Faltings height of the jacobian in two different ways. First, we use a known case of the Colmez conjecture, due to Colmez and Obus, that is valid when the CM field is an abelian extension of the rationals. It links the height and the logarithmic derivatives of an
$2$ curve over a number field whose jacobian has complex multiplication will usually have stable bad reduction at some prime. We prove this by computing the Faltings height of the jacobian in two different ways. First, we use a known case of the Colmez conjecture, due to Colmez and Obus, that is valid when the CM field is an abelian extension of the rationals. It links the height and the logarithmic derivatives of an 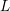 $L$ -function. The second formula involves a decomposition of the height into local terms based on a hyperelliptic model. We use the reduction theory of genus
$L$ -function. The second formula involves a decomposition of the height into local terms based on a hyperelliptic model. We use the reduction theory of genus 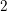 $2$ curves as developed by Igusa, Liu, Saito, and Ueno to relate the contribution at the finite places with the stable bad reduction of the curve. The subconvexity bounds by Michel and Venkatesh together with an equidistribution result of Zhang are used to bound the infinite places.
$2$ curves as developed by Igusa, Liu, Saito, and Ueno to relate the contribution at the finite places with the stable bad reduction of the curve. The subconvexity bounds by Michel and Venkatesh together with an equidistribution result of Zhang are used to bound the infinite places.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 5
- Cited by


