Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-05T14:00:43.810Z Has data issue: false hasContentIssue false
  • English
  • Français

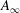$A_{\infty }$-algebras associated with curves and rational functions on 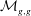$\mathcal{M}_{g,g}$. I

Part of: (Co)homology theory Curves Homological methods Operations and obstructions

Published online by Cambridge University Press:  10 March 2014

Robert Fisette  and
Alexander Polishchuk
Robert Fisette
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA email [email protected]
Alexander Polishchuk
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the natural 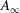$A_{\infty }$-structure on the 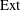$\mathrm{Ext}$-algebra 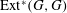$\mathrm{Ext}^*(G,G)$ associated with the coherent sheaf 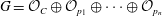$G=\mathcal{O}_C\oplus \mathcal{O}_{p_1}\oplus \cdots \oplus \mathcal{O}_{p_n}$ on a smooth projective curve 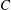$C$, where 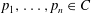$p_1,\ldots,p_n\in C$ are distinct points. We study the homotopy class of the product 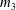$m_3$. Assuming that 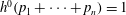$h^0(p_1+\cdots +p_n)=1$, we prove that 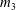$m_3$ is homotopic to zero if and only if 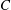$C$ is hyperelliptic and the points 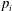$p_i$ are Weierstrass points. In the latter case we show that 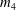$m_4$ is not homotopic to zero, provided the genus of 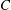$C$ is greater than 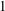$1$. In the case 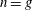$n=g$ we prove that the 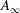$A_{\infty }$-structure is determined uniquely (up to homotopy) by the products 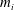$m_i$ with 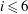$i\le 6$. Also, in this case we study the rational map 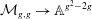$\mathcal{M}_{g,g}\to \mathbb{A}^{g^2-2g}$ associated with the homotopy class of 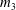$m_3$. We prove that for 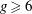$g\ge 6$ it is birational onto its image, while for 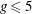$g\le 5$ it is dominant. We also give an interpretation of this map in terms of tangents to 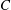$C$ in the canonical embedding and in the projective embedding given by the linear series 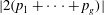$|2(p_1+\cdots +p_g)|$.

Keywords

A∞-structureMassey productsderived categoryHochschild cohomologyalgebraic curve

MSC classification

Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 16E45: Differential graded algebras and applications 14H10: Families, moduli (algebraic) 55S30: Massey products
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 4 , April 2014 , pp. 621 - 667
Copyright
© The Author(s) 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardzell, M. J., The alternating syzygy behavior of monomial algebras, J. Algebra 188 (1997), 69–89.Google Scholar
Bondal, A. and Kapranov, M., Framed triangulated categories, Math. USSR-Sb. 70 (1991), 93–107.Google Scholar
Cohen, J. M., The decomposition of stable homotopy, Ann. of Math. (2) 87 (1968), 305–320.Google Scholar
Efimov, A. I., Homological mirror symmetry for curves of higher genus, Adv. Math. 230 (2012), 493–530.Google Scholar
Fisette, R., The A-infinity algebra of a curve and the $j$-invariant, PhD thesis, University of Oregon, 2012.Google Scholar
Gelfand, S. and Manin, Yu., Methods of homological algebra (Springer, Berlin, 1996).Google Scholar
Green, M. and Lazarsfeld, R., Some results on the syzygies of finite sets and algebraic curves, Compositio Math. 67 (1988), 301–314.Google Scholar
Gugenheim, V. K. A. M. and Stasheff, J. D., On perturbations and A ∞-structures, Bull. Soc. Math. Belg. Ser. A 38 (1986), 237–246.Google Scholar
Gugenheim, V. K. A. M., Lambe, L. A. and Stasheff, J. D., Perturbation theory in differential homological algebra. II, Illinois J. Math. 35 (3) (1991), 357–373.Google Scholar
Hartshorne, R., Deformation theory (Springer, New York, 2010).Google Scholar
Hille, L. and Van den Bergh, M., Fourier-Mukai transforms, in Handbook of tilting theory (Cambridge University Press, Cambridge, 2007), 147–177.Google Scholar
Kadeishvili, T. V., The category of differential coalgebras and the category of A ∞-algebras, Trudy Tbiliss. Mat. Instituta 77 (1985), 50–70; (in Russian).Google Scholar
Kapranov, M., Derived categories of coherent sheaves on homogeneous spaces, Dissertation, Steklov Mathematical Institute, 1988 (in Russian).Google Scholar
Kapustin, A., Katzarkov, L., Orlov, D. and Yotov, M., Homological mirror symmetry for manifolds of general type, Cent. Eur. J. Math. 7 (2009), 571–605.Google Scholar
Keller, B., Introduction to A-infinity algebras and modules, Homology Homotopy Appl. 3 (2001), 1–35.CrossRefGoogle Scholar
Keller, B., A-infinity algebras, modules and functor categories, in Trends in representation theory of algebras and related topics (American Mathematical Society, Providence, RI, 2006), 67–93.Google Scholar
Kontsevich, M. and Soibelman, Y., Homological mirror symmetry and torus fibration, in Symplectic geometry and mirror symmetry (Seoul, 2000) (World Scientific, River Edge, NJ, 2001), 203–263.CrossRefGoogle Scholar
Kraines, D. A., Higher Massey products, Trans. Amer. Math. Soc. 124 (1966), 431–439.Google Scholar
Lekili, Y. and Perutz, T., Fukaya categories of the torus and Dehn surgery, Proc. Natl. Acad. Sci. 108 (2011), 8106–8113.Google Scholar
Lu, D.-M., Palmieri, J. H., Wu, Q.-S. and Zhang, J. J., A-infinity structure on Ext-algebras, J. Pure Appl. Algebra 213 (2009), 2017–2037.Google Scholar
May, J. P., Matric Massey Products, J. Algebra 12 (1969), 533–568.Google Scholar
Merkulov, S., Strong homotopy algebras of a Kähler manifold, Int. Math. Res. Notices (3) (1999), 153–164.Google Scholar
Orlov, D., Remarks on generators and dimensions of triangulated categories, Moscow Math. J. 9 (2009), 153–159.Google Scholar
Polishchuk, A., Extensions of homogeneous coordinate rings to A ∞-algebras, Homology Homotopy Appl. 5 (2003), 407–421.Google Scholar
Polishchuk, A., Triple Massey products on curves, Fay’s trisecant identity and tangents to the canonical embedding, Moscow Math. J. 3 (2003), 105–121.Google Scholar
Polishchuk, A., A ∞-algebra of an elliptic curve and Eisenstein series, Comm. Math. Phys. 301 (2011), 709–722.Google Scholar
Seidel, P., Homological mirror symmetry for the genus two curve, J. Algebraic Geom. 20 (2011), 727–769.Google Scholar
Shipley, B., An algebraic model for rational S 1-equivariant stable homotopy theory, Q. J. Math. 53 (2002), 87–110.Google Scholar
Toën, B., Finitude homotopique des dg-algèbres propres et lisses, Proc. Lond. Math. Soc. (3) 98 (2009), 217–240.CrossRefGoogle Scholar
Wahl, J., Gaussian maps on algebraic curves, J. Differential Geom. 32 (1990), 77–98.Google Scholar