Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T15:02:19.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine cluster monomials are generalized minors

Part of: Linear algebraic groups and related topics Arithmetic rings and other special rings

Published online by Cambridge University Press:  14 June 2019

Dylan Rupel ,
Salvatore Stella  and
Harold Williams
Dylan Rupel
Affiliation:
University of Notre Dame, Department of Mathematics, Notre Dame, IN 46556, USA email [email protected]
Salvatore Stella
Affiliation:
Department of Mathematics, University of Leicester, Leicester LE1 7RH, UK email [email protected]
Harold Williams
Affiliation:
University of California, Davis, Department of Mathematics, Davis, CA 95616, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the realization of acyclic cluster algebras as coordinate rings of Coxeter double Bruhat cells in Kac–Moody groups. We prove that all cluster monomials with 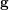$\mathbf{g}$-vector lying in the doubled Cambrian fan are restrictions of principal generalized minors. As a corollary, cluster algebras of finite and affine type admit a complete and non-recursive description via (ind-)algebraic group representations, in a way similar in spirit to the Caldero–Chapoton description via quiver representations. In type 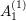$A_{1}^{(1)}$, we further show that elements of several canonical bases (generic, triangular, and theta) which complete the partial basis of cluster monomials are composed entirely of restrictions of minors. The discrepancy among these bases is accounted for by continuous parameters appearing in the classification of irreducible level-zero representations of affine Lie groups. We discuss how our results illuminate certain parallels between the classification of representations of finite-dimensional algebras and of integrable weight representations of Kac–Moody algebras.

Keywords

cluster algebrasKac–Moody groups

MSC classification

Primary: 13F60: Cluster algebras 20G44: Kac-Moody groups
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 7 , July 2019 , pp. 1301 - 1326
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramenko, P. and Brown, K. S., Buildings: theory and applications, Graduate Texts in Mathematics, vol. 248 (Springer, New York, 2008).10.1007/978-0-387-78835-7Google Scholar
Assem, I., Simson, D. and Skowronski, A., Elements of the representation theory of associative algebras, Vol. I (Cambridge University Press, Cambridge, 2006).10.1017/CBO9780511614309Google Scholar
Berenstein, A., Fomin, S. and Zelevinsky, A., Cluster algebras. III. Upper bounds and double Bruhat cells , Duke Math. J. 126 (2005), 1–52.10.1215/S0012-7094-04-12611-9Google Scholar
Berenstein, A. and Zelevinsky, A., Triangular bases in quantum cluster algebras , Int. Math. Res. Not. IMRN 2014 (2014), 1651–1688.10.1093/imrn/rns268Google Scholar
Caldero, P. and Chapoton, F., Cluster algebras as Hall algebras of quiver representations , Comment. Math. Helv. 81 (2006), 595–616.10.4171/CMH/65Google Scholar
Caldero, P. and Keller, B., From triangulated categories to cluster algebras. II , Ann. Sci. Éc. Norm. Supér. (4) 39 (2006), 983–1009.10.1016/j.ansens.2006.09.003Google Scholar
Caldero, P. and Zelevinsky, A., Laurent expansions in cluster algebras via quiver representations , Mosc. Math. J. 6 (2006), 411–429.10.17323/1609-4514-2006-6-3-411-429Google Scholar
Cerulli Irelli, G., Cluster algebras of type A 2 (1) , Algebr. Represent. Theory 15 (2012), 977–1021.10.1007/s10468-011-9275-5Google Scholar
Cerulli Irelli, G. and Esposito, F., Geometry of quiver Grassmannians of Kronecker type and applications to cluster algebras , Algebra Number Theory 5 (2011), 777–801.10.2140/ant.2011.5.777Google Scholar
Chari, V., Integrable representations of affine Lie algebras , Invent. Math. 85 (1986), 317–335.10.1007/BF01389093Google Scholar
Chari, V., Moura, A. and Young, C., Prime representations from a homological perspective , Math. Z. 274 (2013), 613–645.10.1007/s00209-012-1088-7Google Scholar
Chari, V. and Pressley, A., New unitary representations of loop groups , Math. Ann. 275 (1986), 87–104.10.1007/BF01458586Google Scholar
Chari, V. and Pressley, A., Integrable representations of twisted affine Lie algebras , J. Algebra 113 (1988), 438–464.10.1016/0021-8693(88)90171-8Google Scholar
Chari, V. and Pressley, A., Weyl modules for classical and quantum affine algebras , Represent. Theory 5 (2001), 191–223.10.1090/S1088-4165-01-00115-7Google Scholar
Cheung, M. W., Gross, M., Muller, G., Musiker, G., Rupel, D., Stella, S. and Williams, H., The greedy basis equals the theta basis: a rank two haiku , J. Combin. Theory Ser. A 145 (2017), 150–171.10.1016/j.jcta.2016.08.004Google Scholar
Demonet, L., Mutations of group species with potentials and their representations. Applications to cluster algebras, Preprint (2010), arXiv:1003.5078.Google Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations II: Applications to cluster algebras , J. Amer. Math. Soc. 23 (2010), 749–790.10.1090/S0894-0347-10-00662-4Google Scholar
Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras , Mem. Amer. Math. Soc. 6 (1976).Google Scholar
Dupont, G., Generic variables in acyclic cluster algebras , J. Pure Appl. Algebra 215 (2011), 628–641.10.1016/j.jpaa.2010.06.012Google Scholar
Dupont, G., Generic cluster characters , Int. Math. Res. Not. IMRN 2012 (2012), 360–393.10.1093/imrn/rnr024Google Scholar
Dupont, G. and Thomas, H., Atomic bases of cluster algebras of types A and ˜A , Proc. Lond. Math. Soc. (3) 107 (2013), 825–850.10.1112/plms/pdt001Google Scholar
Fomin, S. and Zelevinsky, A., Double Bruhat cells and total positivity , J. Amer. Math. Soc. 12 (1999), 335–380.10.1090/S0894-0347-99-00295-7Google Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations , J. Amer. Math. Soc. 15 (2002), 497–529; (electronic).10.1090/S0894-0347-01-00385-XGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. IV. Coefficients , Compos. Math. 143 (2007), 112–164.10.1112/S0010437X06002521Google Scholar
Gabriel, P., Indecomposable representations. II , in Symposia mathematica, Vol. XI (Academic Press, London, 1973), 81–104.Google Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., Canonical bases for cluster algebras , J. Amer. Math. Soc. 31 (2018), 497–608.10.1090/jams/890Google Scholar
Hubery, A., Acyclic cluster algebras via Ringel–Hall algebras, Preprint,http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.182.6939.Google Scholar
Kac, V. and Peterson, D., Regular functions on certain infinite-dimensional groups , in Arithmetic and geometry, Volume II: Geometry, Progress in Mathematics, vol. 36, eds Artin, M. and Tate, J. (Birkhäuser, Boston, 1983), 141–166.10.1007/978-1-4757-9286-7_8Google Scholar
Kashiwara, M., Crystal bases of modified quantized enveloping algebra , Duke Math. J. 73 (1994), 383–413.10.1215/S0012-7094-94-07317-1Google Scholar
Kumar, S., Kac-Moody groups, their flag varieties, and representation theory, Progress in Mathematics, vol. 204 (Birkhäuser, Boston, 2002).10.1007/978-1-4612-0105-2Google Scholar
Lee, K., Li, L. and Zelevinsky, A., Greedy elements in rank 2 cluster algebras , Selecta Math. (N.S.) 20 (2014), 57–82.10.1007/s00029-012-0115-1Google Scholar
Musiker, G., Schiffler, R. and Williams, L., Bases for cluster algebras from surfaces , Compos. Math. 149 (2013), 217–263.10.1112/S0010437X12000450Google Scholar
Nakanishi, T. and Stella, S., Diagrammatic description of c-vectors and d-vectors of cluster algebras of finite type , Electron. J. Combin. 21 (2014), Paper 1.3, 107.Google Scholar
Nakanishi, T. and Zelevinsky, A., On tropical dualities in cluster algebras , in Algebraic groups and quantum groups, Contemporary Mathematics, vol. 565 (American Mathematical Society, Providence, RI, 2012), 217–226.10.1090/conm/565/11159Google Scholar
Palu, Y., Cluster characters for 2-Calabi–Yau triangulated categories , Ann. Inst. Fourier (Grenoble) 58 (2008), 2221–2248.10.5802/aif.2412Google Scholar
Plamondon, P.-G., Generic bases for cluster algebras from the cluster category , Int. Math. Res. Not. IMRN 2013 (2013), 2368–2420.10.1093/imrn/rns102Google Scholar
Reading, N., Clusters, Coxeter-sortable elements and noncrossing partitions , Trans. Amer. Math. Soc. 359 (2007), 5931–5958.10.1090/S0002-9947-07-04319-XGoogle Scholar
Reading, N. and Speyer, D. E., Combinatorial frameworks for cluster algebras , Int. Math. Res. Not. IMRN 2016 (2016), 109–173.10.1093/imrn/rnv101Google Scholar
Reading, N. and Speyer, D. E., Cambrian frameworks for cluster algebras of affine type , Trans. Amer. Math. Soc. 370 (2018), 1429–1468.10.1090/tran/7193Google Scholar
Reading, N. and Stella, S., An affine almost positive roots model, Preprint (2017),arXiv:1707.00340.Google Scholar
Rupel, D., On a quantum analog of the Caldero–Chapoton formula , Int. Math. Res. Not. IMRN 2011 (2011), 3207–3236.Google Scholar
Rupel, D., Greedy bases in rank 2 generalized cluster algebras, Preprint (2013),arXiv:1309.2567.Google Scholar
Rupel, D., Quantum cluster characters for valued quivers , Trans. Amer. Math. Soc. 367 (2015), 7061–7102.10.1090/S0002-9947-2015-06251-5Google Scholar
Rupel, D. and Stella, S., Some consequences of categorification, Preprint (2017),arXiv:1712.08478.Google Scholar
Rupel, D., Stella, S. and Williams, H., On generalized minors and quiver representations , Int. Math. Res. Not. IMRN 2018 (2018), doi:10.1093/imrn/rny053.Google Scholar
Sherman, P. and Zelevinsky, A., Positivity and canonical bases in rank 2 cluster algebras of finite and affine types , Mosc. Math. J. 4 (2004), 947–974.10.17323/1609-4514-2004-4-4-947-974Google Scholar
Thurston, D. P., Positive basis for surface skein algebras , Proc. Natl. Acad. Sci. USA 111 (2014), 9725–9732.10.1073/pnas.1313070111Google Scholar
Williams, H., Cluster ensembles and Kac–Moody groups , Adv. Math. 247 (2013), 1–40.10.1016/j.aim.2013.07.008Google Scholar
Williams, H., Double Bruhat cells in Kac–Moody groups and integrable systems , Lett. Math. Phys. 103 (2013), 389–419.10.1007/s11005-012-0604-3Google Scholar
Yang, S.-W. and Zelevinsky, A., Cluster algebras of finite type via Coxeter elements and principal minors , Transform. Groups 13 (2008), 855–895.10.1007/s00031-008-9025-xGoogle Scholar