Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-19T21:49:26.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Abelian varieties isogenous to a power of an elliptic curve

Part of: Abelian varieties and schemes Arithmetic algebraic geometry

Published online by Cambridge University Press:  21 March 2018

Bruce W. Jordan ,
Allan G. Keeton ,
Bjorn Poonen ,
Eric M. Rains ,
Nicholas Shepherd-Barron  and
John T. Tate
Bruce W. Jordan
Affiliation:
Department of Mathematics, Baruch College, The City University of New York, One Bernard Baruch Way, New York, NY 10010-5526, USA email [email protected]
Allan G. Keeton
Affiliation:
Center for Communications Research, 805 Bunn Drive, Princeton, NJ 08540-1966, USA email [email protected]
Bjorn Poonen
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA email [email protected]
Eric M. Rains
Affiliation:
Department of Mathematics, California Institute of Technology, Pasadena, CA 91125, USA email [email protected]
Nicholas Shepherd-Barron
Affiliation:
Mathematics Department, King’s College London, Strand, London WC2R 2LS, UK email [email protected]
John T. Tate
Affiliation:
Mathematics Department, Harvard University, 1 Oxford Street, Cambridge MA 02138-2901, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 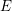$E$ be an elliptic curve over a field 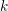$k$. Let 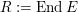$R:=\operatorname{End}E$. There is a functor 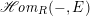$\mathscr{H}\!\mathit{om}_{R}(-,E)$ from the category of finitely presented torsion-free left 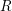$R$-modules to the category of abelian varieties isogenous to a power of 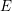$E$, and a functor 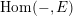$\operatorname{Hom}(-,E)$ in the opposite direction. We prove necessary and sufficient conditions on 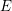$E$ for these functors to be equivalences of categories. We also prove a partial generalization in which 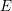$E$ is replaced by a suitable higher-dimensional abelian variety over 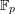$\mathbb{F}_{p}$.

Keywords

Abelian varietyelliptic curveisogeny

MSC classification

Primary: 14K15: Arithmetic ground fields
Secondary: 11G10: Abelian varieties of dimension $> 1$ 14K02: Isogeny 14K05: Algebraic theory
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 5 , May 2018 , pp. 934 - 959
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, M. H., González-Jiménez, E., González, J. and Poonen, B., Finiteness results for modular curves of genus at least 2 , Amer. J. Math. 127 (2005), 1325–1387.Google Scholar
Bass, H., On the ubiquity of Gorenstein rings , Math. Z. 82 (1963), 8–28.Google Scholar
Borevič, Z. I. and Faddeev, D. K., Integral representations of quadratic rings , Vestik Leningrad Univ. 15 (1960), 52–64.Google Scholar
Borevič, Z. I. and Faddeev, D. K., Representations of orders with a cyclic index , Proc. Steklov Inst. Math. 80 (1965), 51–65; translated in Algebraic number theory and representations, ed. D. K. Faddeev (AMS, Washington, DC, 1968), pp. 56–72.Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre. Chapitres 1 á 3 (Hermann, Paris, 1970).Google Scholar
Centeleghe, T. G. and Stix, J., Categories of abelian varieties over finite fields, I: Abelian varieties over F p , Algebra Number Theory 9 (2015), 225–265.Google Scholar
Deligne, P., Variétés abéliennes ordinaires sur un corp fini , Invent. Math. 8 (1969), 238–243.Google Scholar
Eichler, M., Über die Idealklassenzahl hyperkomplexer Systeme , Math. Z. 43 (1938), 481–494.Google Scholar
Giraud, J., Remarque sur une formule de Shimura–Taniyama , Invent. Math. 5 (1968), 231–236.Google Scholar
Grothendieck, A., Techniques de construction et théorèmes d’existence en géomtrie algébrique III: préschemas quotients, Séminaire Bourbaki 13e année, 1960/61, no. 212.Google Scholar
Kani, E., Products of CM elliptic curves , Collect. Math. 62 (2011), 297–339.Google Scholar
Lam, T. Y., Lectures on modules and rings, Graduate Texts in Mathematics, vol. 189 (Springer, New York, 1999).Google Scholar
Lang, S., Algebra, Graduate Texts in Mathematics, vol. 211, revised 3rd edn (Springer, New York, 2002).Google Scholar
Lange, H., Produkte elliptischer Kurven , Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II (1975), 95–108.Google Scholar
Lauter, K., The maximum or minimum number of rational points on genus three curves over finite fields, with an appendix by J.-P. Serre , Compos. Math. 134 (2002), 87–111.CrossRefGoogle Scholar
Levy, L., Modules over Dedekind-like rings , J. Algebra 93 (1985), 1–116.CrossRefGoogle Scholar
Li, K.-Z. and Oort, F., Moduli of supersingular abelian varieties (Springer, Berlin, 1998).CrossRefGoogle Scholar
Mestre, J.-F., La méthode des graphes. Exemples et applications , in Proceedings of the international conference on class numbers and fundamental units of algebraic number fields, Katata, 1986 (Nagoya University, Nagoya, 1986), 217–242.Google Scholar
Mumford, D., Abelian varieties (Tata Institute of Fundamental Research and Oxford University Press, Oxford, 1970).Google Scholar
Ogus, A., Supersingular K3 crystals , in Journées de Géométrie Algébrique de Rennes (Rennes, 1978), Vol. II, Astérisque, vol. 64 (Société Mathématique de France, Paris, 1979), 3–86.Google Scholar
Oort, F., Which abelian surfaces are products of elliptic curves? Math. Ann. 214 (1975), 35–47.Google Scholar
Reiner, I., Maximal orders (Oxford University Press, Oxford, 2003).Google Scholar
Salce, L., Warfield domains: module theory from linear algebra to commutative algebra through abelian groups , Milan J. Math. 70 (2002), 163–185.Google Scholar
Schoen, C., Produkte abelscher Varietäten und Moduln über Ordnungen , J. Reine Angew. Math. 429 (1992), 115–123.Google Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques , Invent. Math. 15 (1972), 259–331.Google Scholar
Serre, J.-P., Rational points on curves over finite fields, Part I: ‘ $q$ large’. Lectures given at Harvard University, September to December 1985, notes taken by Fernando Gouvêa.Google Scholar
Shioda, T., Supersingular K3 surfaces , in Algebraic geometry, Copenhagen 1978, Lecture Notes in Mathematics, vol. 732, ed. Lønsted, K. (Springer, Berlin, 1979), 564–591.Google Scholar
Shioda, T. and Mitani, N., Singular abelian surfaces and binary quadratic forms , in Classification of algebraic varieties and compact complex manifolds, Lecture Notes in Mathematics, vol. 412 (Springer, Berlin, 1974), 259–287.Google Scholar
Tate, J., Endomorphisms of abelian varieties over finite fields , Invent. Math. 2 (1966), 134–144.Google Scholar
Waterhouse, W. C., Abelian varieties over finite fields , Ann. Sci. Éc. Norm. Supér. (4) 2 (1969), 521–560.CrossRefGoogle Scholar
Yu, C.-F., Superspecial abelian varieties over finite prime fields , J. Pure Appl. Algebra 216 (2012), 1418–1427.Google Scholar