Published online by Cambridge University Press: 12 April 2016
In this paper, we will present a high-order, well-conditioned boundary element method (BEM) based on Müller's hypersingular second kind integral equation formulation to accurately compute electrostatic potentials in the presence of inhomogeneity embedded within layered media. We consider two types of inhomogeneities: the first one is a simple model of an ion channel which consists of a finite height cylindrical cavity embedded in a layered electrolytes/membrane environment, and the second one is a Janus particle made of two different semi-spherical dielectric materials. Both types of inhomogeneities have relevant applications in biology and colloidal material, respectively. The proposed BEM gives 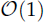 condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.
condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.