Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Jun
Cai, Wei
and
Wu, Xiaoping
2017.
A High-Order Time Domain Discontinuous Galerkin Method with Orthogonal Tetrahedral Basis for Electromagnetic Simulations in 3-D Heterogeneous Conductive Media.
Communications in Computational Physics,
Vol. 21,
Issue. 4,
p.
1065.
Wang, Xiang
Li, Jichun
and
Fang, Zhiwei
2018.
Development and analysis of Crank‐Nicolson scheme for metamaterial Maxwell's equations on nonuniform rectangular grids.
Numerical Methods for Partial Differential Equations,
Vol. 34,
Issue. 6,
p.
2040.
Li, Jichun
Chen, Meng
and
Chen, Min
2019.
Developing and analyzing fourth-order difference methods for the metamaterial Maxwell’s equations.
Advances in Computational Mathematics,
Vol. 45,
Issue. 1,
p.
213.
Li, Jichun
Meng, Chen
and
Huang, Yunqing
2019.
Improved Analysis and Simulation of a Time-Domain Carpet Cloak Model.
Computational Methods in Applied Mathematics,
Vol. 19,
Issue. 2,
p.
359.
Li, Jichun
and
Nan, Bing
2019.
Simulating backward wave propagation in metamaterial with radial basis functions.
Results in Applied Mathematics,
Vol. 2,
Issue. ,
p.
100009.
Huang, Yunqing
Meng, Chen
and
Li, Jichun
2019.
Advances in Mathematical Methods and High Performance Computing.
Vol. 41,
Issue. ,
p.
323.
Li, W.
and
Liang, D.
2020.
The spatial fourth-order compact splitting FDTD scheme with modified energy-conserved identity for two-dimensional Lorentz model.
Journal of Computational and Applied Mathematics,
Vol. 367,
Issue. ,
p.
112428.
Huang, Yunqing
and
Li, Jichun
2020.
Numerical analysis of a finite element method for the electromagnetic concentrator model.
Advances in Computational Mathematics,
Vol. 46,
Issue. 6,
Wang, Jiangxing
2021.
Convergence analysis of an accurate and efficient method for nonlinear Maxwell's equations.
Discrete & Continuous Dynamical Systems - B,
Vol. 26,
Issue. 5,
p.
2429.
Wang, Jiangxing
Zhang, Jiwei
and
Zhang, Zhimin
2021.
A CG–DG method for Maxwell’s equations in Cole–Cole dispersive media.
Journal of Computational and Applied Mathematics,
Vol. 393,
Issue. ,
p.
113480.
Wu, C.
Zeng, H.
Huang, Y.
Yi, N.
and
Yuan, J.
2021.
Superconvergence recovery of cubic edge elements for Maxwell’s equations.
Journal of Computational and Applied Mathematics,
Vol. 389,
Issue. ,
p.
113333.
Li, Jichun
2021.
Two new finite element schemes and their analysis for modeling of wave propagation in graphene.
Results in Applied Mathematics,
Vol. 9,
Issue. ,
p.
100136.
Li, Jichun
Shu, Chi-Wang
and
Yang, Wei
2022.
Development and analysis of two new finite element schemes for a time-domain carpet cloak model.
Advances in Computational Mathematics,
Vol. 48,
Issue. 3,
Yao, Changhui
Sun, Rong
and
Huang, Qiumei
2023.
Global well-posedness and exponential stability for Maxwell's equations under delayed boundary condition in metamaterials.
Journal of Differential Equations,
Vol. 365,
Issue. ,
p.
168.
Huang, Yunqing
Li, Jichun
and
Liu, Xin
2023.
Developing and analyzing an explicit unconditionally stable finite element scheme for an equivalent Bérenger’s PML model.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 57,
Issue. 2,
p.
621.
Li, Jichun
2024.
Recent progress on mathematical analysis and numerical simulations for Maxwell's equations in perfectly matched layers and complex media: a review.
Electronic Research Archive,
Vol. 32,
Issue. 3,
p.
1901.
Huang, Yunqing
Li, Jichun
and
Liu, Xin
2024.
Analysis and application of a local discontinuous Galerkin method for the electromagnetic concentrator model.
Numerical Methods for Partial Differential Equations,
Vol. 40,
Issue. 2,
Huang, Yunqing
Li, Jichun
and
He, Bin
2024.
Developing and Analyzing Some Novel Finite Element Schemes for the Electromagnetic Rotation Cloak Model.
Journal of Scientific Computing,
Vol. 100,
Issue. 1,
Huang, Yunqing
Li, Jichun
Yi, Xuancen
and
Zhao, Haoke
2024.
Analysis and application of a time-domain finite element method for the Drude metamaterial perfectly matched layer model.
Journal of Computational and Applied Mathematics,
Vol. 438,
Issue. ,
p.
115575.


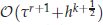 are obtained when polynomials of degree at most
are obtained when polynomials of degree at most 