Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T19:40:33.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle Collisions in a Lumped Particle Model

Published online by Cambridge University Press:  20 August 2015

Omar al-Khayat ,
Are Magnus Bruaset  and
Hans Petter Langtangen
Omar al-Khayat*
Affiliation:
Computational Geosciences, CBC, Simula Research Laboratory, P.O. Box 134, NO-1325 Lysaker, Norway Department of Informatics, University of Oslo, P.O. Box 1080, Blindern, NO-0316 Oslo, Norway
Are Magnus Bruaset*
Affiliation:
Computational Geosciences, CBC, Simula Research Laboratory, P.O. Box 134, NO-1325 Lysaker, Norway Department of Informatics, University of Oslo, P.O. Box 1080, Blindern, NO-0316 Oslo, Norway
Hans Petter Langtangen*
Affiliation:
Department of Informatics, University of Oslo, P.O. Box 1080, Blindern, NO-0316 Oslo, Norway Center for Biomedical Computing, Simula Research Laboratory, P.O. Box 134, NO-1325 Lysaker, Norway
*
Corresponding author.Email:[email protected]
Email:[email protected]
Email:[email protected]
Get access

Abstract

This paper presents an extension of the lumped particle model in [1] to include the effects of particle collisions. The lumped particle model is a flexible framework for the modeling of particle laden flows, that takes into account fundamental features, including advection, diffusion and dispersion of the particles. In this paper, we transform a binary collision model and concepts from kinetic theory into a collision procedure for the lumped particle framework. We apply this new collision procedure to investigate numerically the role of particle collisions in the hindered settling effect. The hindered settling effect is characterized by an increase in the effective drag coefficient CD that influences each particle in the flow. This coefficient is given by 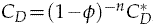, where ϕ is the volume fraction of particles, 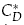is the drag coefficient for a single particle, and n ≃ 4.67 for creeping flow. We obtain an approximation for CD/CD by calculating the effective work done by collisions, and comparing that to the work done by the drag force. In our numerical experiments, we observe a minimal value of n = 3.0. Moreover, by allowing high energy dissipation, an approximation for the classical value for creeping flow, n = 4.7, is reproduced. We also obtain high values for n, up to n = 6.5, which is consistent with recent physical experiments on the sedimentation of sand grains.

Keywords

76M2870F35Lumped particle modelparticle collisionhindered settling
Type
Research Article
Information
Communications in Computational Physics , Volume 10 , Issue 4 , October 2011 , pp. 823 - 843
Copyright
Copyright © Global Science Press Limited 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Khayat, O. al, Bruaset, A. M. and Langtangen, H. P., A lumped particle modeling framework for simulating particle transport in fluids, Commun. Comput. Phys., 8(1) (2010), 115–142.Google Scholar
[2]Alder, B. J. and Wainright, T. E., Studies in molecular dynamics ii, behaviour of small number of elastic spheres, J. Chem. Phys., 33 (1960), 1439–1451.Google Scholar
[3]Chapman, S. and Cowling, T. G., The Mathematical Theory of Non-Uniform Gases, Cambridge University Press, 3rd edition, 1970.Google Scholar
[4]Crowe, C., Sommerfield, M. and Yutaka, T., Multiphase Flows with Droplets and Particles, CRC Press, 1998.Google Scholar
[5]Curtis, J. S. and Wachem, B. van, Modeling particle-laden flows: a research outlook, AIChE J., 50(11) (2004), 2638–2645.Google Scholar
[6]Deen, N. G., Annaland, M. Van Sint, Hoef, M. A. Van der and Kuipers, J. A. M., Review of discrete particle modeling of fluidized beds, Chem. Eng. Sci., 62 (2007), 28–44.Google Scholar
[7]Ding, J. and Gidaspow, D., A bubbling fluidization model using kinetic theory of granular flow, AIChE J., 36 (1990), 523–538.Google Scholar
[8]Felice, R., The void function for fluid-particle interaction systems, Int. J. Multiphase. Flow., 20 (1994), 153–159.CrossRefGoogle Scholar
[9]Foerster, S., Louge, M., Chang, H. and Allia, K., Measurements of the collision properties of small spheres, Phys. Fluids., 6 (1994), 1108–1115.Google Scholar
[10]Goldschmidt, M. J. V., Beetstra, R. and Kuipers, J. A. M., Hydrodynamic modelling of dense gas-fluidised beds: comparison of the kinetic theory of granular flow with 3d hard-sphere discrete particle simulations, Chem. Eng. Sci., 57(11) (2002), 2059–2075.Google Scholar
[11]Gombosi, T. I., Gaskinetic Theory, Cambridge University Press, 1994.Google Scholar
[12]Hales, T. C., Proof of the kepler conjecture, Internet, 1998, http://www.math.pitt.edu/∼th ales/kepler98/.Google Scholar
[13]Helland, E., Bournot, H., Occelli, R. and Tadrist, L., Drag reduction and cluster formation in a circulating fluidised bed, Chem. Eng. Sci., 62(1-2) (2007), 148–158.Google Scholar
[14]Helland, E., Occelli, R. and Tadrist, L., Computational study of fluctuating motions and cluster structures in gas-particle flows, Int. J. Multiphase. Flow., 28 (2002), 199–223.CrossRefGoogle Scholar
[15]Lun, C., Savage, S., Jefferey, D. and Chepurniy, N., Kinetic theories for granular flow: inelastic particles in couette flow and slightly inelastic particles in a general flowfield, J. Fluid. Mech., 140 (1984), 223–256.Google Scholar
[16]Ma, D. and Ahmadi, G., An equation of state for dense rigid sphere gases, J. Chem. Phys., 84 (1960), 3449–3450.Google Scholar
[17]Makkawi, Y. T. and Wright, P. C., The voidage function and effective drag force for fluidized beds, Chem. Eng. Sci., 58 (2003), 2035–2051.CrossRefGoogle Scholar
[18]Maude, A. D. and Whitmore, R. L., A generalized theory of sedimentation, British J. Appl. Phys., 9 (1958), 477–482.Google Scholar
[19]Meiburg, E. and Kneller, B., Turbidity currents and their deposits, Ann. Rev. Fluid. Mech., 42 (2010), 135–156.Google Scholar
[20]Nio, Y. and Garca, M., Using lagrangian particle saltation observations for bedload sediment transport modelling, Hydrol. Process., 12(8) (1998), 1197–1218.Google Scholar
[21]Richardson, J. F. and Zaki, W. N., Sedimentation and fluidization: part I, Trans. Institute. Chem. Eng., 32 (1954), 35–53.Google Scholar
[22]Lee, J. Rodgers and Alan, W.Nicewander, Thirteen ways to look at the correlation coefficient, Am. Stat., 42(1) (1988), 59–66.Google Scholar
[23]Oshima, N., Ogawa, S. and Unemura, A., On the equations of fully fluidized granular materials, Zeitschrift fier Angewandte Mathematik und Mechanik Physics, 31 (1989), 483–493.Google Scholar
[24]Shirolkar, J. S., Coimbra, C. F. M. and McQuay, M. Queroz, Fundemental aspects of modeling turbulent particle dispersion in dilute flows, Pro. Energy. Combust. Sci., 22 (1996), 363–399.Google Scholar
[25]Tomkins, M. R., Baldock, T. E. and Nielsen, P., Hindered settling of sand grains, Sedimentology., 52 (2005), 1425–1432.CrossRefGoogle Scholar
[26]Wachem, B. G. M. van and Almstedt, A. E., Methods for multiphase computational fluid dynamics, Chem. Eng. J., 96(1-3) (2003), 81–98.Google Scholar
[27]Walker, R. G., The origin and significance of the internal sedimentary structures of turbidites, P. Yorks. Geol. Soc., 35 (1965), 1–32.Google Scholar
[28]Wang, S., Li, X., Lu, H., Yu, L., Ding, J. and Yang, Z., DSMC prediction of granular temperatures of clusters and dispersed particles in a riser, Powder. Tech., 192 (2009), 225–233.Google Scholar
[29]Wen, C. Y. and Yu, Y. H., Mechanics of fluidization, Chem. Eng. P. Symp. Ser., 62 (1966), 100–111.Google Scholar