Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T21:06:31.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Solutions of Coupled Nonlinear Schrödinger Equations by Orthogonal Spline Collocation Method

Published online by Cambridge University Press:  20 August 2015

Qing-Jiang Meng ,
Li-Ping Yin ,
Xiao-Qing Jin  and
Fang-Li Qiao
Qing-Jiang Meng*
Affiliation:
Department of Mathematics, University of Macau, Macao
Li-Ping Yin*
Affiliation:
First Institute of Oceanography, State Oceanic Administration, Qingdao, Shandong 266061, China & College of Physical and Environmental Ocanography, Ocean University of China, Qingdao, Shandong 266003, China
Xiao-Qing Jin*
Affiliation:
Department of Mathematics, University of Macau, Macao
Fang-Li Qiao*
Affiliation:
Key Laboratory of Marine Science and Numerical Modeling of State Oceanic Administration & First Institute of Oceanography, State Oceanic Administration, Qingdao, Shandong 266061, China
*
Corresponding author.Email address:[email protected]
Email address:[email protected]
Email address:[email protected]
Email address:[email protected]
Get access

Abstract

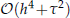In this paper, we present the use of the orthogonal spline collocation method for the semi-discretization scheme of the one-dimensional coupled nonlinear Schrödinger equations. This method uses the Hermite basis functions, by which physical quantities are approximated with their values and derivatives associated with Gaussian points. The convergence rate with order and the stability of the scheme are proved. Conservation properties are shown in both theory and practice. Extensive numerical experiments are presented to validate the numerical study under consideration.

Keywords

65N3535C4535L65Coupled nonlinear Schrödinger equationsorthogonal spline collocation methodconservation law
Type
Research Article
Information
Communications in Computational Physics , Volume 12 , Issue 5 , November 2012 , pp. 1392 - 1416
Copyright
Copyright © Global Science Press Limited 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ablowitz, M. J. and Segur, H., Solitons and the Inverse Scattering Transform, SIAM, Philadelphia, 1981.CrossRefGoogle Scholar
[2]Antoine, X., Arnold, A., Besse, C., Ehrhardt, M. and Schadle, A., A review of transparent and artificial boundary conditions techniques for linear and nonlinear Schrödinger equations, Commun. Comput. Phys., 4 (2008), 729–796.Google Scholar
[3]Bao, W. Z., Ground states and dynamics of multicomponent Bose-Einstein condensates, Multiscale Model. Simul., 2 (2004), 201–236.Google Scholar
[4]Bao, W. Z. and Shen, J., A fourth-order time-splitting Laguerre-Hermite pseudospectral method for Bose-Einstein condensates, SIAM J. Sci. Comput., 26 (2005), 2010–2028.Google Scholar
[5]Bao, W. Z. and Zheng, C. X., A time-splitting spectral method for three-wave interactions in media with competing quadratic and cubic nonlinearities, Commun. Comput. Phys., 2 (2007), 123–140.Google Scholar
[6]Benney, D. J. and Newell, A. C., Random wave closures, Stud. Appl. Math., 48 (1969), 29–53.Google Scholar
[7]de Boor, C. and Swartz, B., Collocation at Gauss points, SIAM. J. Numer. Anal., 10 (1973), 582–606.Google Scholar
[8]Chang, Q. S., Jia, E. H. and Sun, W. W., Difference schemes for solving the generalized nonlinear Schrödinger equation, J. Comput. Phys., 148 (1999), 397–415.Google Scholar
[9]Chen, Y. M., Zhu, H. J. and Song, S. H., Multi-symplectic splitting method for the coupled nonlinear Schrödinger equation, Comput. Phys. Commun., 181 (2010), 1231–1241.CrossRefGoogle Scholar
[10]Douglas, J. Jr and Dupont, T., Collocation Methods for Parabolic Equations in a Single Space Variable, Lecture Notes in Math, Vol. 385, Spring-Verleg, New York, 1974.CrossRefGoogle Scholar
[11]Fairweather, G. and Meade, D., A survey of spline collocation methods for the numerical solution of differential equations, in: Diaz, J. C. ed., Mathematics for Large Scale Computing, Lecture Notes in Pure Appl. Math., Vol. 120, Marcel Dekker, New York, (1989), 297–341.Google Scholar
[12]Guo, B. Y., Pedro, J. P., Maria, J. R. and Luis, V., Numerical solution of the Sine-Gordon equation, Appl. Math. Comput., 18 (1986), 1–14.Google Scholar
[13]Ismail, M. S. and Alamri, S. Z., Highly accurate finite difference method for coupled nonlinear Schrödinger equation, Int. J. Comput. Math., 81 (2004), 333–351.Google Scholar
[14]Ismail, M. S. and Taha, T. R., Numerical simulation of coupled nonlinear Schrödinger equation, Math. Comput. Simul., 56 (2001), 547–562.Google Scholar
[15]Klein, P., Antoine, X., Besse, C. and Ehrhardt, M., Absorbing boundary conditions for solving N-dimensional stationary Schrödinger equations with unbounded potentials and nonlinearities, Commun. Comput. Phys., 10 (2011), 1280–1304.CrossRefGoogle Scholar
[16]Menyuk, C. R., Nonlinear pulse propagation in birefringent optical fibers, IEEE J. Quantum Electron., 23 (1987), 174–176.Google Scholar
[17]Robinson, M. P. and Fairweather, G., Orthogonal spline collocation methods for Schrödinger-type equations in one space variable, Numer. Math., 68 (1994), 355–376.CrossRefGoogle Scholar
[18]Sun, J. Q., Gu, X. Y. and Ma, Z. Q., Numerical study for the soliton waves of the coupled nonlinear Schrödinger system, Phys. D, 196 (2004), 311–328.Google Scholar
[19]Sun, J. Q. and Qin, M. Z., Multi-symplectic methods for the coupled 1D nonlinear Schrödinger system, Comput. Phys. Commun., 155 (2003), 221–235.CrossRefGoogle Scholar
[20]Thalhammer, M., Caliari, M. and Neuhauser, C., High-order time-splitting Hermite and Fourier spectral methods, J. Comput. Phys., 228 (2009), 822–832.Google Scholar
[21]Utsumi, T., Aoki, T., Koga, J. and Yamagiwa, M., Solutions of the 1D coupled nonlinear schrödinger equations by the CIP-BS method, Commun. Comput. Phys., 1 (2006), 261–275.Google Scholar
[22]Ueda, T. and Kath, W. L., Dynamics of coupled solitons in nonlinear optical fibers, Phys. Rev. A, 42 (1990), 563–571.Google Scholar
[23]Wang, H. Q., Numerical studies on the split step finite difference method for the nonlinear Schrödinger equations, Appl. Math. Comput., 170 (2005), 17–35.Google Scholar
[24]Wadati, M., Izuka, T. and Hisakado, M., A coupled nonlinear Schrödinger equation and optical solitons, J. Phys. Soc. Jpn., 61 (1992), 2241–2245.Google Scholar
[25]Xu, Y. and Shu, C. W., Local discontinuous Galerkin methods for nonlinear Schrödinger equations, J. Comput. Phys., 205 (2005), 72–97.Google Scholar
[26]Xu, Y. and Shu, C. W., Local discontinuous Galerkin methods for high-order time-dependent partial differential equations, Commun. Comput. Phys., 7 (2010), 1–46.Google Scholar
[27]Xu, Y. and Shu, C. W., Local discontinuous Galerkin methods for the Degasperis-Procesi equation, Commun. Comput. Phys., 10 (2011), 474–508.Google Scholar
[28]Yang, J. K., Multisoliton perturbation theory for the Manakov equations and its applications to nonlinear optics, Phys. Rev. E, 59 (1999), 2393–2405.CrossRefGoogle Scholar
[29]Yang, J. K. and Benney, D. J., Some properties of nonlinear wave systems, Stud. Appl. Math., 96 (1996), 111–135.Google Scholar
[30]Zhang, Y. Z., Bao, W. Z. and Li, H. L., Dynamics of rotating two-component Bose-Einstein condensates and its efficient computation, Phys. D, 234 (2007), 49–69.Google Scholar