Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T03:23:52.388Z Has data issue: false hasContentIssue false
  • English
  • Français

A Novel Efficient Numerical Solution of Poisson's Equation for Arbitrary Shapes in Two Dimensions

Part of: Numerical approximation and computational geometry Polytopes and polyhedra

Published online by Cambridge University Press:  02 November 2016

Zu-Hui Ma ,
Weng Cho Chew  and
Li Jun Jiang
Zu-Hui Ma*
Affiliation:
Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong
Weng Cho Chew*
Affiliation:
Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801 USA
Li Jun Jiang*
Affiliation:
Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong
*
*Corresponding author. Email addresses:[email protected] (Z.-H. Ma), [email protected] (W. C. Chew), [email protected] (L. J. Jiang)
*Corresponding author. Email addresses:[email protected] (Z.-H. Ma), [email protected] (W. C. Chew), [email protected] (L. J. Jiang)
*Corresponding author. Email addresses:[email protected] (Z.-H. Ma), [email protected] (W. C. Chew), [email protected] (L. J. Jiang)
Get access

Abstract

Even though there are various fast methods and preconditioning techniques available for the simulation of Poisson problems, little work has been done for solving Poisson's equation by using the Helmholtz decomposition scheme. To bridge this issue, we propose a novel efficient algorithm to solve Poisson's equation in irregular two dimensional domains for electrostatics through a quasi-Helmholtz decomposition technique—the loop-tree basis decomposition. It can handle Dirichlet, Neumann or mixed boundary problems in which the filling media can be homogeneous or inhomogeneous. A novel point of this method is to first find the electric flux efficiently by applying the loop-tree basis functions. Subsequently, the potential is obtained by finding the inverse of the gradient operator. Furthermore, treatments for both Dirichlet and Neumann boundary conditions are addressed. Finally, the validation and efficiency are illustrated by several numerical examples. Through these simulations, it is observed that the computational complexity of our proposed method almost scales as 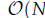, where N is the triangle patch number of meshes. Consequently, this new algorithm is a feasible fast Poisson solver.

Keywords

Fast Poisson solverloop-tree decompositionelectrostatics

MSC classification

Secondary: 52B10: Three-dimensional polytopes 65D18: Computer graphics, image analysis, and computational geometry 68U05: Computer graphics; computational geometry 68U07: Computer-aided design
Type
Research Article
Information
Communications in Computational Physics , Volume 20 , Issue 5 , November 2016 , pp. 1381 - 1404
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Datta, S., Quantum Transport: Atom to Transistor, 2nd Edition, Cambridge University Press, 2005.CrossRefGoogle Scholar
[2] Fogolari, F., Brigo, A., Molinari, H., The poissonboltzmann equation for biomolecular electrostatics: a tool for structural biology, Journal of Molecular Recognition 15 (6) (2002) 377–392.CrossRefGoogle ScholarPubMed
[3] Elman, H. C., Silvester, D. J., Wathen, A. J., Finite elements and fast iteratice solvers with applications in incompressible fluidd dynamics, Oxford university press, New York, 2005.CrossRefGoogle Scholar
[4] Feynman, R. P., Leighton, R. B., Sands, M., The Feynman Lectures on Physics including Feynman's Tips on Physics: The Definitive and Extended Edition, 2nd Edition, Addison Wesley, 2005.Google Scholar
[5] Andrei, P., Mayergoyz, I., Analysis of fluctuations in semiconductor devices through self-consistent poisson-schrödinger computations, Journal of Applied Physics 96 (4) (2004) 2071–2079.Google Scholar
[6] Luscombe, J. H., Bouchard, A. M., Luban, M., Electron confinement in quantum nanostructures: Self-consistent poisson-schrödinger theory, Phys. Rev. B 46 (1992) 10262–10268.CrossRefGoogle ScholarPubMed
[7] Cheng, C., Lee, J.-H., Lim, K. H., Massoud, H. Z., Liu, Q. H., 3d quantum transport solver based on the perfectly matched layer and spectral element methods for the simulation of semiconductor nanodevices, Journal of Computational Physics 227 (1) (2007) 455–471.Google Scholar
[8] Jiang, H., Shao, S., Cai, W., Zhang, P., Boundary treatments in non-equilibrium greens function (negf) methods for quantum transport in nano-mosfets, Journal of Computational Physics 227 (13) (2008) 6553–6573.Google Scholar
[9] Huang, J. Z., Chew, W. C., Tang, M., Jiang, L., Efficient simulation and analysis of quantum ballistic transport in nanodevices with awe, IEEE Trans. on Electron Devices 59 (2) (2012) 468–476.CrossRefGoogle Scholar
[10] Sköllermo, G., A fourier method for the numerical solution of poisson's equations, Mathmatics of Computation 29 (131) (1975) 697–711.Google Scholar
[11] Lai, M., Wang, W., Fast direct solvers for poisson equation on 2d polar and spherical geometries, Numerical Methods for Partial Differential Equations 18 (1) (2002) 56–68.Google Scholar
[12] Huang, Y.-L., Liu, J.-G., Wang, W.-C., An fft based fast poisson solver on spherical shells, Communications in Computational Physics 9 (3, SI) (2011) 649–667.CrossRefGoogle Scholar
[13] Davis, T. A., Duff, I. S., An unsymmetric-pattern multifrontal method for sparse lu factorization, SIAM Journal on Matrix Analysis and Applications 18 (1) (1997) 140–158.Google Scholar
[14] McKenney, A., Greengard, L., Mayo, A., A fast poisson solver for complex geometries, Journal of Computational Physics 118 (2) (1995) 348–355.Google Scholar
[15] Huang, J., Greengard, L., A fast direct solver for elliptic partial differential equations on adaptively refined meshes, SIAM J. Sci. Copmut. 21 (4) (1999) 1551–1566.Google Scholar
[16] Ethridge, F., Greengard, L., A new fast-multipole accelerated poisson solver in two dimensions, SIAM J. Sci. Copmut. 23 (3) (2001) 741–760.Google Scholar
[17] Langston, M. H., Greengard, L., Zorin, D., A free-space adaptive fmm-based pde solver in three dimensions, Communications in Applied Mathematics and Computational Science 6 (1) (2011) 79–122.CrossRefGoogle Scholar
[18] Brandt, A., Multi-Level Adaptive Solutions to Boundary-Value Problems, Mathematics of Computation 31 (138) (1977) 333–390.Google Scholar
[19] Yavneh, I., Why multigrid methods are so efficient, Computing in Science Engineering 8 (6) (2006) 12–22.Google Scholar
[20] Brandt, A., Livne, O., Multigrid Techniques: 1984 Guide with Applications to Fluid Dynamics, Classics in applied mathematics, Society for Industrial and Applied Mathematics (SIAM, 3600 Market Street, Floor 6, Philadelphia, PA 19104), 2011.Google Scholar
[21] Trottenberg, U., Oosterlee, C.W., Schller, A., Multigrid, Academic Press, 2001.Google Scholar
[22] Fulton, S. R., Ciesielski, P. E., Schubert, W. H., Multigrid methods for elliptic problems: A review, Monthly Weather Review 14 (1986) 943–959.2.0.CO;2>CrossRefGoogle Scholar
[23] Briggs, L., Henson, V. E., McCormick, S. F., A Multigrid Tutorial, SIAM, Philadelphia, 2000.Google Scholar
[24] Peskin, C. S., Numerical analysis of blood flowin the heart, Journal of Computational Physics 25 (3) (1977) 220–252.CrossRefGoogle Scholar
[25] Fedkiw, R. P., Aslam, T., Merriman, B., Osher, S., A non-oscillatory eulerian approach to interfaces in multimaterial flows (the ghost fluid method), Journal of Computational Physics 152 (2) (1999) 457–492.Google Scholar
[26] Kafafy, R., Lin, T., Lin, Y., Wang, J., Three-dimensional immersed finite element methods for electric field simulation in composite materials, International Journal for Numerical Methods in Engineering 64 (7) (2005) 940–972.Google Scholar
[27] Zhang, L., Gerstenberger, A., Wang, X., Liu, W. K., Immersed finite element method, Computer Methods in Applied Mechanics and Engineering 193 (2122) (2004) 2051–2067.Google Scholar
[28] Yu, S., Wei, G., Three-dimensional matched interface and boundary (mib) method for treating geometric singularities, Journal of Computational Physics 227 (1) (2007) 602–632.Google Scholar
[29] LeVeque, R., Li, Z., The immersed interface method for elliptic equations with discontinuous coefficients and singular sources, SIAM Journal on Numerical Analysis 31 (4) (1994) 1019–1044.Google Scholar
[30] Chen, T., Strain, J., Piecewise-polynomial discretization and krylov-accelerated multigrid for elliptic interface problems, Journal of Computational Physics 227 (16) (2008) 7503–7542.Google Scholar
[31] A correction function method for poisson problems with interface jump conditions, Journal of Computational Physics 230 (20) (2011) 7567–7597.Google Scholar
[32] Brown, R. M., The mixed problem for laplace's equation in a class of lipschitz domains, Comm. Partial Diff. Eqns. 19 (1994) 1217–1233.Google Scholar
[33] Rao, S., Wilton, D., Glisson, A., Electromagnetic scattering by surfaces of arbitrary shape, Antennas and Propagation, IEEE Transactions on 30 (3) (1982) 409–418.Google Scholar
[34] Bladel, J. G. V., Electromagnetic Fields, Wiley-IEEE Press, 2007.Google Scholar
[35] Wilton, D. R., Glisson, A.W., On improving the electric field integral equation at low frequencies, in: 1981 Spring URSI Radio Science Meeting Digest, Los Angeles, CA, 1981, p. 24.Google Scholar
[36] Mautz, J., Harrington, R., An e-field solution for a conducting surface small or comparable to the wavelength, Antennas and Propagation, IEEE Transactions on 32 (4) (1984) 330–339.Google Scholar
[37] Zhao, J.-S., Chew, W. C., Integral equation solution of maxwell's equations from zero frequency to microwave frequencies, Antennas and Propagation, IEEE Transactions on 48 (10) (2000) 1635–1645.Google Scholar
[38] Wu, W., Glisson, A. W., Kajfez, D., A comparison of two low-frequency formulations for the electric field integral equation, in: Tenth Ann. Rev. Prog. Appl. Comput. Electromag., Vol. 2, 1994, pp. 484–491.Google Scholar
[39] Burton, M., Kashyap, S., A study of a recent, moment-method algorithm that is accurate to very low frequencies, Appl. Comput. Electromagn. Soc. J. 10 (3) (1995) 58–68.Google Scholar
[40] Chew, W. C., Tong, M. S., Hu, B., Integral Equations Methods for Electromagnetic and Elastic Waves, Morgan & Claypool, 2008.Google Scholar
[41] Vecchi, G., Loop-star decomposition of basis functions in the discretization of the efie, Antennas and Propagation, IEEE Transactions on 47 (2) (1999) 339–346.Google Scholar
[42] Hanson, G. W., Yakovlev, A. B., Operator theory for electromagnetics, Springer-Verlag, New York, 2001.Google Scholar
[43] Ma, Z.-H., Chew, W. C., Jiang, L., A novel fast solver for poisson's equation with the neumann boundary condition, Progress In Electromagnetics Research 136 (2013) 195–209.Google Scholar
[44] Chew, W. C., Waves and Fields in Inhomogeneous Media, IEEE Press, NJ, 1995.Google Scholar
[45] van der Vorst, H. A., Bi-cgstab: A fast and smoothly converging variant of bi-cg for the solution of nonsymmetric linear systems, SIAM J. on Scientific Computing 13 (1992) 631–644.Google Scholar
[46] Saad, Y., Iterative Methods for Sparse Linear Systems, 2nd Edition, Society for Industrial and Applied Mathematics, 2003.Google Scholar
[47] Saad, Y., Schultz, M., Gmres: A generalized minimal residue algorithm for solving nonsymmetric linear systems, SIAM J. Sci. Stat. Comput. 7 (1986) 856–869.Google Scholar