Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T08:32:43.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonconforming Finite Element Method Applied to the Driven Cavity Problem

Part of: Partial differential equations, boundary value problems Numerical methods

Published online by Cambridge University Press:  08 March 2017

Roktaek Lim  and
Dongwoo Sheen
Roktaek Lim*
Affiliation:
Division of Mathematical Sciences, School of Physical & Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, Singapore 637371
Dongwoo Sheen*
Affiliation:
Department of Mathematics, Seoul National University, Seoul 08826, Korea
*
*Corresponding author. Email addresses:[email protected] (R. Lim), [email protected] (D. Sheen)
*Corresponding author. Email addresses:[email protected] (R. Lim), [email protected] (D. Sheen)
Get access

Abstract

A cheapest stable nonconforming finite element method is presented for solving the incompressible flow in a square cavity without smoothing the corner singularities. The stable cheapest nonconforming finite element pair based on P1×P0 on rectangularmeshes [29] is employed with a minimal modification of the discontinuous Dirichlet data on the top boundary, where 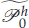is the finite element space of piecewise constant pressures with the globally one-dimensional checker-board pattern subspace eliminated. The proposed Stokes elements have the least number of degrees of freedom compared to those of known stable Stokes elements. Three accuracy indications for our elements are analyzed and numerically verified. Also, various numerous computational results obtained by using our proposed element show excellent accuracy.

Keywords

Nonconforming finite element methodincompressible Navier-Stokes equationslid driven cavity problem

MSC classification

Secondary: 65N30: Finite elements, Rayleigh-Ritz and Galerkin methods, finite methods 74S05: Finite element methods
Type
Research Article
Information
Communications in Computational Physics , Volume 21 , Issue 4 , April 2017 , pp. 1012 - 1038
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Jie Shen

References

[1] Incompressible Flow & Iterative Solver Software. http://www.maths.manchester.ac.uk/djs/ifiss.Google Scholar
[2] Altmann, R. and Carstensen, C.. Generalized Park-Sheen Finite Elements for Adaptivity. PAMM Proc. Appl. Math. Mech., 12(1): 659–660, 2012.Google Scholar
[3] Altmann, R. and Carstensen, C.. P 1-nonconforming finite elements on triangulations into triangles and quadrilaterals. SIAM Journal on Numerical Analysis, 50(2):418–438, 2012.Google Scholar
[4] Auteri, F., Parolini, N., and Quartapelle, L.. Numerical investigation on the stability of singular driven cavity flow. Journal of Computational Physics, 183(1):1–25, 2002.Google Scholar
[5] Aydin, M. and Fenner, R.. Boundary element analysis of driven cavity flow for low and moderate Reynolds number. Int. J. Numer. Meth. Fluids., 37:45–64, 2001.Google Scholar
[6] Barragy, E. and Carey, G.. Stream function-vorticity driven cavity solution using p finite elements. Computers & Fluids, 26:453–468, 1997.Google Scholar
[7] Bercovier, M. and Pironneau, O.. Error estimates for finite element method solution of the Stokes problem in the primitive variables. Numer. Math., 33(2):211–224, 1979.Google Scholar
[8] Botella, O. and Peyret, R.. Benchmark spectral results on the lid-driven cavity flow. Computers & Fluids, 27(4):421–433, 1998.Google Scholar
[9] Bruneau, C.-H. and Saad, M.. The 2D lid–driven cavity problem revisited. Computers & Fluids, 35(3):326–348, 2006.Google Scholar
[10] Cai, Z., Douglas, J. Jr., Santos, J. E., Sheen, D., and Ye, X.. Nonconforming quadrilateral finite elements: A correction. Calcolo, 37(4):253–254, 2000.Google Scholar
[11] Cai, Z., Douglas, J. Jr., and Ye, X.. A stable nonconforming quadrilateral finite element method for the stationary Stokes and Navier-Stokes equations. Calcolo, 36:215–232, 1999.Google Scholar
[12] Cai, Z. and Wang, Y.. An error estimate for two-dimensional Stokes driven cavity flow. Math. Comp., 78:771–787, 2009.CrossRefGoogle Scholar
[13] Crouzeix, M. and Raviart, P.-A.. Conforming and nonconforming finite element methods for solving the stationary Stokes equations. R.A.I.R.O.–Math. Model. Anal. Numer., 7:33–75, 1973.Google Scholar
[14] Cuvelier, C., Segal, A., and Van Steenhoven, A. A.. Finite element methods and Navier–Stokes equations, volume 22. Springer, 1986.Google Scholar
[15] Douglas, J. Jr., Santos, J. E., Sheen, D., and Ye, X.. Nonconforming Galerkin methods based on quadrilateral elements for second order elliptic problems. ESAIM–Math. Model. Numer. Anal., 33(4):747–770, 1999.Google Scholar
[16] Elman, H., Silvester, D., and Wathen, A.. Finite elements and fast iterative solvers: with applications in incompressible fluid dynamics. Oxford University Press, 2014.Google Scholar
[17] Erturk, E.. Discussions on driven cavity flow. International Journal for Numerical Methods in Fluids, 60(3):275–294, 2009.Google Scholar
[18] Erturk, E., Corke, T. C., and Gökçöl, C.. Numerical solutions of 2-D steady incompressible driven cavity flow at high Reynolds numbers. International Journal for Numerical Methods in Fluids, 48(7):747–774, 2005.Google Scholar
[19] Ghia, U., Ghia, K. N., and Shin, C. T.. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comp. Phys., 48:387–411, 1982.CrossRefGoogle Scholar
[20] Glowinski, R.. Finite element methods for incompressible viscous flow. In Ciarlet, P. G. and Lions, J. L., editors, Handbook of Numerical Analysis. IX. Numerical Methods for Fluids (Part 3). Elsevier/North-Holland, Amsterdam, 2003.Google Scholar
[21] Glowinski, R., Guidoboni, G., and Pan, T.-W.. Wall-driven incompressible viscous flow in a two-dimensional semi-circular cavity. J. Comp. Phys., 216(1):76–91, 2006.Google Scholar
[22] Guermond, J.-L. and Minev, P.. A new class of massively parallel direction splitting for the incompressible Navier–Stokes equations. Computer Methods in Applied Mechanics and Engineering, 200(23):2083–2093, 2011.Google Scholar
[23] Guermond, J.-L. and Minev, P. D.. A new class of fractional step techniques for the incompressible Navier–Stokes equations using direction splitting. Comptes Rendus Mathematique, 348(9):581–585, 2010.Google Scholar
[24] Guermond, J.-L. and Minev, P. D.. Start-up flow in a three-dimensional lid-driven cavity by means of amassively parallel direction splitting algorithm. International Journal for Numerical Methods in Fluids, 68(7):856–871, 2012.CrossRefGoogle Scholar
[25] Hood, P. and Taylor, C.. A numerical solution of the Navier–Stokes equations using the finite element techniques. Computers & Fluids, 1:73–100, 1973.Google Scholar
[26] Jeon, Y., Nam, H., Sheen, D., and Shim, K.. A class of nonparametric DSSY nonconforming quadrilateral elements. ESAIM–Math. Model. Numer. Anal., 47(6):1783–1796, 2013.Google Scholar
[27] Karakashian, O. A.. On a Galerkin–Lagrange multiplier method for the stationary Navier–Stokes equations. SIAM J. Numer. Anal., 19(5):909–923, 1982.Google Scholar
[28] Karakashian, O. A. and Jureidini, W. N. A Nonconforming Finite Element Method for the Stationary Navier–Stokes Equations. SIAM J. Numer. Anal., 35(1):93–120, 1998.CrossRefGoogle Scholar
[29] Kim, S., Yim, J., and Sheen, D.. Stable cheapest nonconforming finite elements for the Stokes equations. J. Comput. Appl. Math., 299:2–14, 2016.Google Scholar
[30] Lee, Y.–J. and Li, H.. Axisymmetric Stokes equations in polygonal domains: Regularity and finite element approximations. Comput. Math. Appl., 64:3500–3521, 2012.CrossRefGoogle Scholar
[31] Park, C.. A study on locking phenomena in finite element methods. PhD thesis, Department of Mathematics, Seoul National University, Korea, Feb. 2002. Available at http://www.nasc.snu.ac.kr/cpark/papers/phdthesis.ps.gz.Google Scholar
[32] Park, C. and Sheen, D.. P 1-nonconforming quadrilateral finite element methods for secondorder elliptic problems. SIAM J. Numer. Anal., 41(2):624–640, 2003.Google Scholar
[33] Rannacher, R. and Turek, S.. Simple nonconforming quadrilateral Stokes element. Numer. Methods Partial Differential Equations, 8:97–111, 1992.Google Scholar
[34] Sahin, M. and Owens, R.. A novel fully implicit finite volume methods applied to the lid-driven cavity problem–Part I: High Reynolds number flow calculations. Int. J. Numer. Meth. Fluids., 42:57–77, 2003.CrossRefGoogle Scholar
[35] Serre, D.. Équations de Navier-Stokes stationnaires avec données peu régulières. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze, 10(4): 543–559, 1983 Google Scholar
[36] Shen, J.. Hopf bifurcation of the unsteady regularized driven cavity flow. J. Comp. Phys., 95:228–245, 1991.Google Scholar