Published online by Cambridge University Press: 20 August 2015
We propose a direct solver for the three-dimensional Poisson equation with a variable coefficient, and an algorithm to directly solve the associated sparse linear systems that exploits the sparsity pattern of the coefficient matrix. Introducing some appropriate finite difference operators, we derive a second-order scheme for the solver, and then two suitable high-order compact schemes are also discussed. For a cube containing N nodes, the solver requires 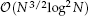 arithmetic operations and
arithmetic operations and 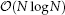 memory to store the necessary information. Its efficiency is illustrated with examples, and the numerical results are analysed.
memory to store the necessary information. Its efficiency is illustrated with examples, and the numerical results are analysed.