Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T06:18:31.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Enslaved Phase-Separation Fronts and Liesegang Pattern Formation

Published online by Cambridge University Press:  20 August 2015

E. M. Foard  and
A. J. Wagner
E. M. Foard*
Affiliation:
Department of Physics, North Dakota State University, Fargo, ND 58105, USA
A. J. Wagner*
Affiliation:
Department of Physics, North Dakota State University, Fargo, ND 58105, USA
*
Corresponding author.Email:[email protected]
Email:[email protected]
Get access

Abstract

We show that an enslaved phase-separation front moving with diffusive speeds 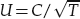can leave alternating domains of increasing size in their wake. We find the size and spacing of these domains is identical to Liesegang patterns. For equal composition of the components we are able to predict the exact form of the pattern analytically. To our knowledge this is the first fully analytical derivation of the Liesegang laws. We also show that there is a critical value for C below which only two domains are formed. Our analytical predictions are verified by numerical simulations using a lattice Boltzmann method.

Keywords

35B3665Z0574S3076T99Liesegangphase separationfrontreaction diffusionpattern formationlattice BoltzmannMatalon-Packter
Type
Research Article
Information
Communications in Computational Physics , Volume 9 , Issue 5 , May 2011 , pp. 1081 - 1093
Copyright
Copyright © Global Science Press Limited 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Antal, T., Droz, M., Magnin, J., and Rácz, Z., Formation of liesegang patterns: a spinodal decomposition scenario, Phys. Rev. Lett., 83(15) (1999), 2880–2883.CrossRefGoogle Scholar
[2]Antal, T., Droz, M., Magnin, J., Rácz, Z., and Zrinyi, M., Derivation of the matalon-packter law for liesegang patterns, J. Chem. Phys., 109 (1998), 9479–9486.Google Scholar
[3]Chopard, B., Luthi, P., and Droz, M., Reaction-diffusion cellular-automata model for the formation of liesegang patterns, Phys. Rev. Lett., 72(9) (1994), 1384–1387.Google Scholar
[4]Foard, E. M., and Wagner, A. J., Enslaved phase-separation fronts in one-dimensional binary mixtures, Phys. Rev. E., 79(5) (2009), 056710.Google Scholar
[5]Izsak, F., and Lagzi, I., Simulation of liesegang pattern formation using a discrete stochastic model, Chem. Phys. Lett., 371(3-4) (2003), 321–326.Google Scholar
[6]Jablczynski, K., La formation rythmique des pecipites: les anneaux de liesegang, Bull. Soc. Chim. Fr., 33 (1923), 1592.Google Scholar
[7]Jahnke, L., and Kantelhardt, J. W., Comparison of models and lattice-gas simulations for liesegang patterns, Euro. Phys. J. Special Topics., 161 (2008), 121–141.Google Scholar
[8]Liesegang, R. E., Ueber einige eigenschaften von gallertenm, Naturwissenschaftliche Wochenschrift, 11(30) (1896), 353–362.Google Scholar
[9]Racz, Z., Formation of Liesegang patterns, Phys. A., 274(1-2) (1999), 50–59.Google Scholar
[10]Stern, K. H., The Liesegang phenomenon, Chem. Rev., 54 (1954), 79–99.Google Scholar
[11]Wagner, A. J., and Pooley, C. M., Interface width and bulk stability: requirements for the simulation of deeply quenched liquid-gas systems, Phys. Rev. E., 76(4) (2007), 045702.CrossRefGoogle ScholarPubMed