Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-02T23:10:28.307Z Has data issue: false hasContentIssue false
  • English
  • Français

An Iterative Discontinuous Galerkin Method for Solving the Nonlinear Poisson Boltzmann Equation

Published online by Cambridge University Press:  03 June 2015

Peimeng Yin ,
Yunqing Huang  and
Hailiang Liu
Peimeng Yin*
Affiliation:
Hunan Key Laboratory for Computation and Simulation in Science and Engineering; School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, P.R. China
Yunqing Huang*
Affiliation:
Hunan Key Laboratory for Computation and Simulation in Science and Engineering; School of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, P.R. China
Hailiang Liu*
Affiliation:
Iowa State University, Mathematics Department, Ames, IA 50011, USA
*
Email:[email protected]
Email:[email protected]
Corresponding author.Email:[email protected]
Get access

Abstract

An iterative discontinuous Galerkin (DG) method is proposed to solve the nonlinear Poisson Boltzmann (PB) equation. We first identify a function space in which the solution of the nonlinear PB equation is iteratively approximated through a series of linear PB equations, while an appropriate initial guess and a suitable iterative parameter are selected so that the solutions of linear PB equations are monotone within the identified solution space. For the spatial discretization we apply the direct discontinuous Galerkin method to those linear PB equations. More precisely, we use one initial guess when the Debye parameter λ = 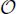(1), and a special initial guess for λ ≫1 to ensure convergence. The iterative parameter is carefully chosen to guarantee the existence, uniqueness, and convergence of the iteration. In particular, iteration steps can be reduced for a variable iterative parameter. Both one and two-dimensional numerical results are carried out to demonstrate both accuracy and capacity of the iterative DG method for both cases of λ = 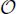(1) and λ ≪ 1. The (m + 1)th order of accuracy for L2 and mth order of accuracy for H1 for Pm elements are numerically obtained.

Keywords

65D1565N3035J0535J25Poisson-Boltzmann equationnonlinearexistenceuniquenessDDG methodsnumerical flux.
Type
Research Article
Information
Communications in Computational Physics , Volume 16 , Issue 2 , August 2014 , pp. 491 - 515
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Holst, M., McCammom, J. A., Yu, Z., Zhou, Y. C., Zhu, Y.Adaptive finite element modeling techniques for the Poisson-Boltzmann equation. Commun. Comput. Phys., 11(1):179–214, 2012/01.Google Scholar
[2]Debye, P., Hiickel, E.Zur theorie der elektrolyte. Phys. Zeitschr., 24: 185–206, 1923.Google Scholar
[3]Kirkwood, J. G.On the theory of strong electrolyte solutions. J. Chem. Phys., 2:767–781, 1934.Google Scholar
[4]Boschitsch, A. H., Fenley, M. O.Hybrid boundary element and finite difference method for solving the nonlinear Poisson-Boltzmann equation. J. Comput. Chem., 25(7):935–955, 2004.Google Scholar
[5]Baker, N. A., Sept D., D., Joseph, S., Holst, M. J., McCammon, J. A.Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA, 98:10037–10041,2001.Google Scholar
[6]Qiao, Z.-H., Li, Z.-L., Tang, T.A finite difference scheme for solving the nonlinear Poisson-Boltzmann equation modeling charged spheres. J. Comput. Math., 24(3):252–264,2006/03.Google Scholar
[7]Colella, Phillip, Dorr, Milo R, Wake, Daniel D. A conservative finite difference method for the numerical solution of plasma fluid equations. J. Comput. Phys., 149(1): 168–193, 1999.Google Scholar
[8]Chen, L., Holst, M. J., Xu, J.The finite element approximation of the nonlinear Poisson-Boltzmann equation. SIAM J. Numer. Anal., 45(6): 2298–2320, 2007.Google Scholar
[9]Lu, B., Cheng, X., Huang, J.AFMPB: An adaptive fast multipole Poisson-Boltzmann solver for calculating electrostatics in biomolecular systems. C. Phys. Commun., 181(6):1150–1160, 2010.Google Scholar
[10]Degond, P., Liu, H., Savelief, D., Vignal, M. H.Numerical approximation of the Euler-Poisson-Boltzmann model in the quasineutral limit. J. Sci. Comput., 51: 59–86, 2012.Google Scholar
[11]Liu, H., Yan, J.The Direct Discontinuous Galerkin (DDG) method for diffusion problems. SIAM Journal on Numerical Analysis., 47(1): 675–698,2009.CrossRefGoogle Scholar
[12]Liu, H., Yan, J.The Direct Discontinuous Galerkin (DDG) method for diffusion with interface corrections. Commun. Comput. Phys., 8(3): 541–564,2010.Google Scholar
[13]Huang, Y., Liu, H., Yi, N.Recovery of normal derivatives from the piecewise L2 projection. J. Comput. Phys., 231(4): 1230–1243, 2012.Google Scholar
[14]Oberoi, H., Allewell, N. M.Multigrid solution of the nonlinear Poisson-Boltzmann equation and calculation of titration curves. Biophys J., 65(1): 48–55, 1993.Google Scholar
[15]Nicholls, A., Honig, B.A rapid finite difference algorithm, utilizing successive overrelaxation to solve the Poisson-Boltzmann equation. Journal of Computational Chemistry, 12(4): 435–445, 1991.CrossRefGoogle Scholar
[16]Davis, M. E., McCammon, J. A.Solving the finite difference linearized Poisson-Boltzmann equation: A comparison of relaxation and conjugate gradient methods. Journal of Computational Chemistry, 10(3): 386–391, 1989.CrossRefGoogle Scholar
[17]Deng, Y., Chen, G., Ni, W., Zhou, J.Boundary element monotone iteration scheme for semilinear elliptic partial differential equations. Mathematics of Computation, 65(215):943–982, 1996.Google Scholar
[18]Shampine, L. F.Monotone iterations and two-sided convergence. SIAM Journal on Numerical Analysis, 3(4): 607–615, 1996.Google Scholar
[19]Chern, I., Liu, J., Wang, W.Accurate evaluation of electrostatics for macromolecules in solution. Methods and Applications of Analysis, 10(2): 309–328, 2003.Google Scholar
[20]Quarteroni, A., Valli, A.Numerical approximation of partial differential equations. Springer Series in Computational Mathematics, 2008.Google Scholar
[21]Evans, L. C.Partial differential equations. American Mathematics Society, 19, 2010.Google Scholar
[22]Lions, J. L., Magenes, E.Non-Homogeneous Boundary Value Problems and Applications. New-York: Springer-Verlag, 1972.Google Scholar
[23]Liu, H., Yu, H.The entropy satisfying discontinuous Galerkin method for Fokker-Planck equations. Journal on Scientific Computing, accepted (2014).Google Scholar
[24]Liu, H.Optimal error estimates of the Direct Discontinuous Galerkin method for convection-diffusion equations. Math. Comp., to appear (2014).Google Scholar