Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T17:04:57.220Z Has data issue: false hasContentIssue false
  • English
  • Français

Accurate Simulation of Circular and Elliptic Cylindrical Invisibility Cloaks

Published online by Cambridge University Press:  24 March 2015

Zhiguo Yang  and
Li-Lian Wang
Zhiguo Yang
Affiliation:
Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, 637371, Singapore
Get access

Abstract

The coordinate transformation offers a remarkable way to design cloaks that can steer electromagnetic fields so as to prevent waves from penetrating into the cloaked region (denoted by Ω0, where the objects inside are invisible to observers outside). The ideal circular and elliptic cylindrical cloaked regions are blown up from a point and a line segment, respectively so the transformed material parameters and the corresponding coefficients of the resulted equations are highly singular at the cloaking boundary ∂Ω0. The electric field or magnetic field is not continuous across ∂Ω0. The imposition of appropriate cloaking boundary conditions (CBCs) to achieve perfect concealment is a crucial but challenging issue.

Based upon the principle that a well-behaved electromagnetic field in the original space must be well-behaved in the transformed space as well, we obtain CBCs that intrinsically relate to the essential “pole” conditions of a singular transformation. We also find that for the elliptic cylindrical cloak, the CBCs should be imposed differently for the cosine-elliptic and sine-elliptic components of the decomposed fields. With these at our disposal, we can rigorously show that the governing equation in Ω0 can be decoupled from the exterior region 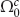, and the total fields in the cloaked region vanish under mild conditions. We emphasize that our proposal of CBCs is different from any existing ones.

Using the exact circular (resp., elliptic) Dirichlet-to-Neumann (DtN) non-reflecting boundary conditions to reduce the unbounded domain 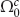to a bounded domain, we introduce an accurate and efficient Fourier-Legendre spectral-element method (FLSEM) (resp., Mathieu-Legendre spectral-element method (MLSEM)) to simulate the circular cylindrical cloak (resp., elliptic cylindrical cloak). We provide ample numerical results to demonstrate that the perfect concealment of waves can be achieved for the ideal circular/elliptic cylindrical cloaks under our proposed CBCs and accurate numerical solvers.

Keywords

65Z0574J2078A4033E1035J0565M7065N35Invisibility cloakssingular coordinate transformationscloaking boundary conditionsessential “pole” conditionsMathieu functionsspectral-element methodsexact Dirichlet-to-Neumann (DtN) boundary conditionsperfect invisibility
Type
Research Article
Information
Communications in Computational Physics , Volume 17 , Issue 3 , March 2015 , pp. 822 - 849
Copyright
Copyright © Global-Science Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abramowitz, M. and Stegun, I.A., editors. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. A Wiley-Interscience Publication. John Wiley & Sons Inc., New York, 1984. Reprint of the 1972 edition, Selected Government Publications.Google Scholar
[2]Adams, R.A. and Fournier, J.J.. Sobolev Spaces, volume 140. Academic press, 2003.Google Scholar
[3]Al-Gwaiz, M.A.. Sturm-Liouville Theory and Its Applications. Springer Undergraduate Mathematics Series. Springer-Verlag, London, 2008.Google Scholar
[4]Ammari, H., Garnier, J., Jing, W.J., Kang, H., Lim, M., Sølna, K., and Wang, H.. Mathematical and Statistical Methods for Multistatic Imaging. Lecture Notes in Mathematics, Vol. 2098, Springer, 2013.Google Scholar
[5]Ammari, H., Garnier, J., Jugnon, V., Kang, H., Lee, H., and Lim, M.. Enhancement of near-cloaking. Part III: Numerical simulations, statistical stability, and related questions. Contemp. Math., 577:1–24, 2012.CrossRefGoogle Scholar
[6]Ammari, H., Kang, H., Lee, H., and Lim, M.. Enhancement of near-cloaking. Part II: the Helmholtz equation. Commun. Math. Phys, 317(2):485–502, 2013.Google Scholar
[7]Ammari, H., Kang, H., Lee, H., Lim, M., and Yu, S.. Enhancement of near cloaking for the full Maxwell equations. SIAM J. Appl. Math., 73(6):2055–2076, 2013.Google Scholar
[8]Berenger, J.P.. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys., 114(2):185–200, 1994.Google Scholar
[9]Boyd, J.P.. Chebyshev and Fourier Spectral Methods. Dover Publications, second edition, 2001.Google Scholar
[10]Cai, W.S. and Shalaev, V.M.. Optical Metamaterials, volume 10. Springer, 2010.Google Scholar
[11]Chen, H.Y.. Transformation optics in orthogonal coordinates. J. Opt. A: Pure Appl. Opt., 11(7):75–102, 2009.Google Scholar
[12]Chen, H.Y., Chan, C.T., and Sheng, P.. Transformation optics and metamaterials. Nature Materials, 9(5):387–396, 2010.CrossRefGoogle ScholarPubMed
[13]Cojocaru, E.. Exact analytical approaches for elliptic cylindrical invisibility cloaks. J. Opt. Soc. Am. B., 26(5):1119–1128, 2009.Google Scholar
[14]Courant, R. and Hilbert, D.. Methods of Mathematical Physics. Vol. I. Interscience Publishers, Inc., New York, N.Y., 1953.Google Scholar
[15]Cui, T.J., Smith, D.R., and Liu, R.P.. Metamaterials: Theory, Design, and Applications. Springer, 2009.Google Scholar
[16]Cummer, S., Popa, B., Schurig, D., Smith, D., and Pendry, J.. Full-wave simulations of electromagnetic cloaking structures. Phys. Rev. E, 74(3):036621, 2006.Google Scholar
[17]Diatta, A., Nicolet, A., Guenneau, S., and Zolla, F.. Tessellated and stellated invisibility. Optics Express, 17(16):13389–13394, 2009.CrossRefGoogle ScholarPubMed
[18]Fang, Q., Nicholls, D.P., and Shen, J.. A stable, high–order method for two–dimensional bounded–obstacle scattering. J. Comput. Phys., 224:1145–1169, 2007.CrossRefGoogle Scholar
[19]Fang, Q., Shen, J., and Wang, L.L.. An efficient and accurate spectral method for acoustic scattering in elliptic domains. Numer. Math.: Theory, Methods Appl., 2:258–274, 2009.Google Scholar
[20]Fleury, R. and Alù, A.. Cloaking and invisibility: A review. Forum for Electromagnetic Research Methods and Application Technologies (FERMAT), 1(7):1–24, 2014.Google Scholar
[21]Gottlieb, D. and Orszag, S.A.. Numerical Analysis of Spectral Methods: Theory and Applications. SIAM-CBMS, Philadelphia, 1977.Google Scholar
[22]Greenleaf, A., Kurylev, Y., Lassas, M., and Uhlmann, G.. Cloaking devices, electromagnetic wormholes, and transformation optics. SIAM Review, 51(1):3–33, 2009.Google Scholar
[23]Greenleaf, A., Lassas, M., and Uhlmann, G.. On nonuniqueness for Calderon’s inverse problem. Math. Res. Lett., 10(5/6):685–694, 2003.Google Scholar
[24]Grote, M.J. and Keller, J.B.. On non-reflecting boundary conditions. J. Comput. Phys., 122:231–243, 1995.Google Scholar
[25]Hao, Y. and Mittra, R.. FDTD Modeling of Metamaterials: Theory and Applications. Artech House, 2008.Google Scholar
[26]Ji, Y.Y., Wu, H., Ma, H.P., and Guo, B.Y.. Multidomain pseudospectral methods for nonlinear convection-diffusion equations. Appl. Math. Mech. (English Ed.), 32(10):1255–1268, 2011.Google Scholar
[27]Jiang, W.X., Cui, T.J., Yu, G.X., Lin, X.Q., Cheng, Q., and Chin, J.Y.. Arbitrarily elliptical–cylindrical invisible cloaking. J. Phys. D: Appl. Phys., 41(8):085504, 2008.Google Scholar
[28]Kohn, R.V., Onofrei, D., Vogelius, M.S., and Weinstein, M.I.. Cloaking via change of variables for the Helmholtz equation. Comm. Pure Appl. Math., 63(8):973–1016, 2010.Google Scholar
[29]Kown, D.H.. Transformation electromagnetics and optics. Forum for Electromagnetic Research Methods and Application Technologies (FERMAT), 1(8):1–11, 2014.Google Scholar
[30]Kwon, D.H. and Werner, D.H.. Two-dimensional eccentric elliptic electromagnetic cloaks. Appl. Phys. Lett, 92(1):013505, 2008.Google Scholar
[31]Lassas, M. and Zhou, T.. Singular partial differential operators and pseudo-differential boundary conditions in invisibility cloaking. In Fourier Analysis, Trends in Mathematics, pages 263–284, 2014. Springer, Switzerland.Google Scholar
[32]Lassas, M. and Zhou, T.. Two dimensional invisibility cloaking for Helmholtz equation and non-local boundary conditions. Math. Res. Lett., 18(3):473–488, 2011.Google Scholar
[33]Leonhardt, U.. Optical conformal mapping. Science, 312(5781):1777–1780, 2006.Google Scholar
[34]Leonhardt, U. and Philbin, T.. Geometry and Light: The Science of Invisibility. Dover Publications, 2012.Google Scholar
[35]Li, J.C. and Huang, Y.Q.. Mathematical simulation of cloaking metamaterial structures. Adv. Appl. Math. Mech, 4:93–101, 2012.Google Scholar
[36]Li, J.C. and Huang, Y.Q.. Time-Domain Finite Element Methods for Maxwell’s Equations in Metamaterials, volume 43. Springer, 2012.Google Scholar
[37]Li, J.C., Huang, Y.Q., and Yang, W.. Developing a time-domain finite-element method for modeling of electromagnetic cylindrical cloaks. J. Comput. Phys., 231(7):2880–2891, 2012.CrossRefGoogle Scholar
[38]Li, J.C., Huang, Y.Q., and Yang, W.. Well-posedness study and finite element simulation of time-domain cylindrical and elliptical cloaks. Math. Comp., In press, 2014.Google Scholar
[39]Li, J.Z., Liu, H.Y., and Sun, H.P.. Enhanced approximate cloaking by SH and FSH lining. Inverse Problems, 28(7):075011, 2012.Google Scholar
[40]Liu, H.Y. and Sun, H.P.. Enhanced near-cloak by FSH lining. J. Math. Pures Appl., 99(1):17–42, 2013.Google Scholar
[41]Liu, H.Y. and Zhou, T.. On approximate electromagnetic cloaking by transformation media. SIAM J. Appl. Math., 71(1):218–241, 2011.Google Scholar
[42]Luo, Y., He, L.X., Zhu, S.Z., and Wang, Y.. Arbitrary polygonal cloaks with multiple invisible regions. J. Modern Opt., 58(1):14–20, 2011.Google Scholar
[43]Ma, H., Qu, S.B., Xu, Z., Zhang, J.Q., Chen, B.W., and Wang, J.F.. Material parameter equation for elliptical cylindrical cloaks. Phys. Rev. A, 77(1):013825, 2008.Google Scholar
[44]McLachlan, N.W.. Theory and Application of Mathieu Functions, volume 4. Dover New York, 1964.Google Scholar
[45]Mechel, F.P.. Formulas of Acoustics, volume 2. Springer, 2002.Google Scholar
[46]Monk, P.. Finite Element Methods for Maxwell’s Equations. Numerical Mathematics and Scientific Computation. Oxford University Press, New York, 2003.Google Scholar
[47]Nédélec, J.C.. Mixed finite elements in R3. Numer. Math., 35(3):315–341, 1980.Google Scholar
[48]Nédélec, J.C.. Acoustic and Electromagnetic Equations, volume 144 of Applied Mathematical Sciences. Springer-Verlag, New York, 2001. Integral representations for harmonic problems.Google Scholar
[49]Orfanidis, S.J.. Electromagnetic Waves and Antennas. Rutgers University, 2002.Google Scholar
[50]Pendry, J. B., Schurig, D., and Smith, D. R.. Controlling electromagnetic fields. Science, 312(5781):1780–1782, 2006.CrossRefGoogle ScholarPubMed
[51]Ruan, Z., Yan, M., Neff, C.W., and Qiu, M.. Ideal cylindrical cloak: perfect but sensitive to tiny perturbations. Phys. Rev. Lett., 99(11):113903, 2007.Google Scholar
[52]Schurig, D., Mock, J., Justice, B., Cummer, S., Pendry, J., Starr, A., and Smith, D.. Metamaterial electromagnetic cloak at microwave frequencies. Science, 314(5801):977–980, 2006.Google Scholar
[53]Shen, J.. Efficient spectral-Galerkin methods III. polar and cylindrical geometries. SIAM J. Sci. Comput., 18:1583–1604, 1997.CrossRefGoogle Scholar
[54]Shen, J., Tang, T., and Wang, L.L.. Spectral Methods: Algorithms, Analysis and Applications, volume 41 of Springer Series in Computational Mathematics. Springer-Verlag, Berlin, Heidelberg, 2011.Google Scholar
[55]Shen, J. and Wang, L.L.. Spectral approximation of the Helmholtz equation with high wave numbers. SIAM J. Numer. Anal., 43(2):623–644, 2005.Google Scholar
[56]Shen, J. and Wang, L.L.. Analysis of a spectral-Galerkin approximation to the Helmholtz equation in exterior domains. SIAM J. Numer. Anal., 45(5):1954–1978, 2007.Google Scholar
[57]Shen, J., Wang, L.L., and Li, H.Y.. A triangular spectral element method using fully tensorial rational basis functions. SIAM J. Numer. Anal., 47(3):1619–1650, 2009.Google Scholar
[58]Wang, L.L., Wang, B., and Zhao, X.D.. Fast and accurate computation of time-domain acoustic scattering problems with exact nonreflecting boundary conditions. SIAM J. Appl. Math., 72(6):1869–1898, 2012.Google Scholar
[59]Watson, G.N.. A Treatise of the Theory of Bessel Functions (second edition). Cambridge University Press, Cambridge, UK, 1966.Google Scholar
[60]Weder, R.. The boundary conditions for point transformed electromagnetic invisibility cloaks. J. Phys. A: Math. Theor., 41(41):415401, 2008.Google Scholar
[61]Werner, D.H. and Kwon, D.H.. Transformation Electromagnetics and Metamaterials: Fundamental Principles and Applications. Springer, 2014.Google Scholar
[62]Whittaker, E.T. and Watson, G.N.. A Course of Modern Analysis. Cambridge university press, 1927.Google Scholar
[63]Wu, Q., Zhang, K., Meng, F.Y., and Li, L.W.. Material parameters characterization for arbitrary N-sided regular polygonal invisible cloak. J. Phys. D: Appl. Phys., 42(3):035408, 2009.Google Scholar
[64]Zhai, Y.B., Ping, X.W., Jiang, W.X., and Cui, T.J.. Finite-element analysis of three-dimensional axisymmetrical invisibility cloaks and other metamaterial devices. Commun. Comput. Phys., 8(4):823–834, 2010.Google Scholar
[65]Zhang, B.L.. Electrodynamics of transformation-based invisibility cloaking. Light: Science & Applications, 1(10):e32, 2012.Google Scholar
[66]Zhang, B.L., Chen, H.S., Wu, B., Luo, Y., Ran, L., and Kong, J.A.. Response of a cylindrical invisibility cloak to electromagnetic waves. Phys. Rev. B, 76(12):121101, 2007.Google Scholar
[67]Zolla, F., Guenneau, S., Nicolet, A., and Pendry, J.B.. Electromagnetic analysis of cylindrical invisibility cloaks and the mirage effect. Optics Letters, 32(9):1069–1071, 2007.CrossRefGoogle ScholarPubMed