Article contents
A Novel Numerical Method of 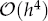 for Three-Dimensional Non-Linear Triharmonic Equations
for Three-Dimensional Non-Linear Triharmonic Equations
Published online by Cambridge University Press: 20 August 2015
Abstract
In this article, we present two new novel finite difference approximations of order two and four, respectively, for the three dimensional non-linear triharmonic partial differential equations on a compact stencil where the values of u, ∂2u/∂n2 and ∂4u/∂n4 are prescribed on the boundary. We introduce new ideas to handle the boundary conditions and there is no need to discretize the derivative boundary conditions. We require only 7- and 19-grid points on the compact cell for the second and fourth order approximation, respectively. The Laplacian and the biharmonic of the solution are obtained as by-product of the methods. We require only system of three equations to obtain the solution. Numerical results are provided to illustrate the usefulness of the proposed methods.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Global Science Press Limited 2012
References
- 3
- Cited by


