Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T13:54:47.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Efficient Implementation of Smoothed Particle Hydrodynamics (SPH) with Plane Sweep Algorithm

Part of: Basic methods in fluid mechanics Algorithms - Computer Science Equations of mathematical physics and other areas of application Coupling of solid mechanics with other effects Numerical approximation and computational geometry

Published online by Cambridge University Press:  16 March 2016

Dong Wang ,
Yisong Zhou  and
Sihong Shao
Dong Wang
Affiliation:
State Key Laboratory of ASIC and System, School of Microelectronics, Fudan University, Shanghai 201203, China
Yisong Zhou
Affiliation:
LMAM and School of Mathematical Sciences, Peking University, Beijing 100871, China
Sihong Shao*
Affiliation:
LMAM and School of Mathematical Sciences, Peking University, Beijing 100871, China
*
*Corresponding author. Email addresses:, [email protected] (D. Wang), [email protected] (Y. Zhou), [email protected] (S. Shao)
Get access

Abstract

Neighbour search (NS) is the core of any implementations of smoothed particle hydrodynamics (SPH). In this paper,we present an efficient 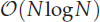neighbour search method based on the plane sweep (PW) algorithm with N being the number of SPH particles. The resulting method, dubbed the PWNS method, is totally independent of grids (i.e., purely meshfree) and capable of treating variable smoothing length, arbitrary particle distribution and heterogenous kernels. Several state-of-the-art data structures and algorithms, e.g., the segment tree and the Morton code, are optimized and implemented. By simply allowingmultiple lines to sweep the SPH particles simultaneously from different initial positions, a parallelization of the PWNS method with satisfactory speedup and load-balancing can be easily achieved. That is, the PWNS SPH solver has a great potential for large scale fluid dynamics simulations.

Keywords

Smoothed particle hydrodynamicsmeshfreemethodneighbour searchplane sweep algorithmMorton codesegment treequadtreeparallelizationdam break

MSC classification

Secondary: 76M28: Particle methods and lattice-gas methods 74F10: Fluid-solid interactions (including aero- and hydro-elasticity, porosity, etc.) 35Q30: Navier-Stokes equations 68W05: Nonnumerical algorithms 65D18: Computer graphics, image analysis, and computational geometry
Type
Research Article
Information
Communications in Computational Physics , Volume 19 , Issue 3 , March 2016 , pp. 770 - 800
Copyright
Copyright © Global-Science Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Lucy, L. B., A numerical approach to the testing of the fission hypothesis, Astron. J. 82 (1977) 1013–1024.CrossRefGoogle Scholar
[2]Gingold, R. A., Monaghan, J. J., Smoothed particle hydrodynamics: theory and application to non-spherical stars, Mon. Not. Roy. Astron. Soc. 181 (1977) 375–389.CrossRefGoogle Scholar
[3]Monaghan, J. J., Simulating free suface flows with SPH, J. Comput. Phys. 110 (1994) 399–406.CrossRefGoogle Scholar
[4]Monaghan, J. J., SPH without a tensile instability, J. Comput. Phys. 159 (2000) 290–311.CrossRefGoogle Scholar
[5]Colagrossi, A., Landrini, M., Numerical simulation of interfacial flows by smoothed particle hydrodynamics, J. Comput. Phys. 191 (2003) 448–475.CrossRefGoogle Scholar
[6]Springel, V., Hernquist, L., Cosmological smoothed particle hydrodynamics simulations: a hybrid multiphase model for star formation, Mon. Not. Roy. Astron. Soc. 339 (2003) 289–311.CrossRefGoogle Scholar
[7]Hu, X. Y., Adams, N. A., A multi-phase SPH method for macroscopic and mesoscopic flows, J. Comput. Phys. 213 (2006) 844–861.CrossRefGoogle Scholar
[8]Monaghan, J. J., A turbulence model for smoothed particle hydrodynamics, Eur. J. Mech. B-Fluids 30 (2011) 360–370.CrossRefGoogle Scholar
[9]Price, D. J., Smoothed particle hydrodynamics and magnetohydrodynamics, J. Comput. Phys. 231 (2012) 759–794.CrossRefGoogle Scholar
[10]Ulrich, C., Leonardi, M., Rung, T., Multi-physics SPH simulation of complex marineengineering hydrodynamic problems, Ocean Eng. 64 (2013) 109–121.CrossRefGoogle Scholar
[11]Cleary, P., Ha, J., Alguine, V., Nguyen, T., Flow modelling in casting processes, Appl. Math. Model. 26 (2002) 171–190.CrossRefGoogle Scholar
[12]Wang, D., Shao, S., Yan, C., Cai, W., Zeng, X., Feature-scale simulations of particulate slurry flows in chemical mechanical polishing by smoothed particle hydrodynamics, Commun. Comput. Phys. 16 (2014) 1389–1418.CrossRefGoogle Scholar
[13]Bentley, J. L., A survey of techniques for fixed radius near neighbor searching, Tech. Rep. SLAC-186, Stanford University, Stanford, CA (1975).Google Scholar
[14]Monaghan, J. J., Particle methods for hydrodynamics, Comput. Phys. Rep. 3 (1985) 71–124.CrossRefGoogle Scholar
[15]Gomez-Gesteira, M., Rogers, B. D., Crespo, A. J. C., Dalrymple, R. A., Narayanaswamy, M., Domínguez, J.M., SPHysics-development of a free-surface fluid solver-Part 2: Efficiency and test cases, Comput. Geosci. 48 (2012) 300–307.CrossRefGoogle Scholar
[16]Hernquist, L., Katz, N., TreeSPH: A unification of SPH with the hierarchical tree method, Astrophys. J. Suppl. Ser. 70 (1989) 419–446.CrossRefGoogle Scholar
[17]Benz, W., Bowers, R. L., Cameron, A. G. W., Press, W. H., Dynamics mass exchange in doubly degenerate binaries. I. 0.9 and 1.2 M ⊙ stars, Astron. J. 348 (1990) 647–667.CrossRefGoogle Scholar
[18]Springel, V., The cosmological simulation code GADGET-2, Mon. Not. Roy. Astron. Soc. 364 (2005) 1105–1134.CrossRefGoogle Scholar
[19]Guo, X., Lind, S., Rogers, B. D., Stansby, P. K., Ashworth, M., Efficient massive parallelisation for incompressible smoothed particle hydrodynamics with 108 particles, in: 8th Int. SPHERICWorkshop, Trondheim, Norway, 2013.Google Scholar
[20]Goswami, P., Schlegel, P., Solenthaler, B., Pajarola, R., Interactive SPH simulation and rendering on the GPU, in: Proc. 2010 ACM SIGGRAPH/Eurograph. Symp. Comput. Anim., Madrid, Spain, 2010, pp. 55–64.Google Scholar
[21]Ďurikovič, J. Onderik, Efficient neighbor search for particle-based fluids, J. Appl.Math. Stat. Inform. 4.Google Scholar
[22]Adams, B., Wicke, M., Meshless approximation methods and applications in physics based modeling and animation, in: Eurograph. Tutor., 2009, pp. 213–239.Google Scholar
[23]Awile, O., Büyükkeçeci, F., Rebouxa, S., Sbalzarini, I. F., Fast neighbor lists for adaptive-resolution particle simulations, Comput. Phys. Commun. 183 (2012) 1073–1081.CrossRefGoogle Scholar
[24]Feldman, J., Bonet, J., Dynamic refinement and boundary contact forces in SPH with applications in fluid flow problems, Int. J. Numer. Methods Eng. 72 (2007) 295324.CrossRefGoogle Scholar
[25]Barcaroloa, D. A., Le Touzé, D., Oger, G., de Vuyst, F., Adaptive particle refinement and derefinement applied to the smoothed particle hydrodynamics method, J. Comput. Phys. 273 (2014) 640–657.CrossRefGoogle Scholar
[26]Barnes, J., Hut, P., A hierarchical O(NlogN) force-calculation algorithm, Nature 324 (1986) 446–449.CrossRefGoogle Scholar
[27]Lee, D. T., Wong, C. K., Worst-case analysis for region and partial region searches in multidimensional binary search trees and balanced quad trees, Acta Inform. 9 (1977) 23–29.CrossRefGoogle Scholar
[28]Davé, R., Dubinski, J., Hernquist, L., Parallel TreeSPH, New Astron. 2 (1997) 277–297.CrossRefGoogle Scholar
[29]Yu, J., Turk, G., Reconstructing surfaces of particle-based fluids using anisotropic kernels, ACM Trans. Gr. 32 (2013) 5:1–5:12.CrossRefGoogle Scholar
[30]Shamos, M. I., Hoey, D., Geometric intersection problems, in: 17thAnnu. Symp. Found. Comput. Sci., Houston, TX, USA, 1976, pp. 208–215.Google Scholar
[31]Alpert, C. J., Mehta, D. P., Sapatnekar, S. S. (Eds.), Handbook of Algorithms for Physical Design Automation, CRC Press, 2008.Google Scholar
[32]Rigaux, P., Scholl, M. O., Voisard, A., Spatial Databases: With Application to GIS, Morgan Kaufmann, 2002.Google Scholar
[33]Morton, G. M., A computer oriented geodetic data base and a new technique in file sequencing, IBM, Ottawa, Canada, 1966.Google Scholar
[34]de Berg, M., Cheong, O., van Kreveld, M., Overmars, M., Computational Geometry - Algorithms and Applications, 3rd Edition, Springer-Verlag Berlin Heidelberg, Berlin, Germany, 2008.CrossRefGoogle Scholar
[35]Wyllie, J. C., The Complexity of Parallel Computations, Ph.D. thesis, Cornell University (1979).Google Scholar
[36]Anderson, R. J., Miller, G. L., Deterministic parallel list ranking, Algorithmica 6 (1991) 859–868.CrossRefGoogle Scholar
[37]Finkel, R. A., Bentley, J. L., Quad trees: A data structure for retrieval on composite keys, Acta Inform. 4 (1974) 1–9.CrossRefGoogle Scholar
[38]Bentley, J. L.,Multidimensional binary search trees used for associative searching, Commun. ACM 18 (1975) 509–517.CrossRefGoogle Scholar
[39]Fenk, R., The BUB-tree, in: Proc. 28th Int. Conf. VLDB, Hong Kong, 2002.Google Scholar
[40]Bayer, R., The universal B-tree for multidimensional indexing: General concepts, in: Proc. Int. Conf.WWCA ‘97, Tsukuba, Japan, 1997, pp. 198–209.CrossRefGoogle Scholar
[41]Bayer, R., McCreight, E. M., Organization and maintenance of large ordered indexes, Acta Inform. 1 (1972) 173–189.CrossRefGoogle Scholar
[42]Tropf, H., Herzog, H., Multidimentional range search in dynamically balanced trees, Angewandte Informatik 2 (1981) 71–77.Google Scholar
[43]Hoare, C. A. R., Quicksort, Comput. J. 5 (1962) 10–16.CrossRefGoogle Scholar
[44]Knuth, D. E., The Art of Computer Programming: Sorting and Searching, Vol. 2, Addison-Wesley, Boston, USA, 1998.Google Scholar
[45]Verlet, L., Computer “experiments” on classical fluids. I. Thermodynamical properties of Lenard-Jones molecules, Phys. Rev. 159 (1967) 98–103.CrossRefGoogle Scholar
[46]Shi, H., J. Schaeffer, , Parallel sorting by regular sampling, J. Parallel Distrib. Comput. 14 (2006) 361–372.CrossRefGoogle Scholar
[47]Agarwal, A., Performance tradeoffs inmultithreaded processors, IEEE Trans. Parallel Distrib. Syst. 3 (1992) 525–539.CrossRefGoogle Scholar
[48]Helmbold, D. P., McDowell, C. E., Modelling speedup (n) greater than n, IEEE Trans. Parallel Distrib. Syst. 1 (1990) 250–256.CrossRefGoogle Scholar
[49]Kleefsman, K., Fekken, G., Veldman, A., Iwanowski, B., Buchner, B., A volume-of-fluid based simulation method for wave impact problems, J. Comput. Phys. 206 (2005) 363–393.CrossRefGoogle Scholar
[50]Adami, S., Hu, X. Y., Adams, N. A., A generalized wall boundary condition for smoothed particle hydrodynamics, J. Comput. Phys. 231 (2012) 7057–7075.CrossRefGoogle Scholar
[51]Gargantini, I., An effective way to represent quadtrees, Commun. ACM 25 (1982) 905–910.CrossRefGoogle Scholar