Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Horng, Tzyy-Leng
and
Teng, Chun-Hao
2012.
An error minimized pseudospectral penalty direct Poisson solver.
Journal of Computational Physics,
Vol. 231,
Issue. 6,
p.
2498.
Ma, Zu-Hui
Chew, Weng Cho
and
Jiang, Li Jun
2016.
A Novel Efficient Numerical Solution of Poisson's Equation for Arbitrary Shapes in Two Dimensions.
Communications in Computational Physics,
Vol. 20,
Issue. 5,
p.
1381.


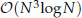 operations. Numerical examples have confirmed the accuracy and robustness of the new scheme.
operations. Numerical examples have confirmed the accuracy and robustness of the new scheme.