Article contents
An Adaptive Finite Element Method with Hybrid Basis for Singularly Perturbed Nonlinear Eigenvalue Problems
Published online by Cambridge University Press: 01 February 2016
Abstract
In this paper, we propose an uniformly convergent adaptive finite element method with hybrid basis (AFEM-HB) for the discretization of singularly perturbed nonlinear eigenvalue problems under constraints with applications in Bose-Einstein condensation (BEC) and quantum chemistry. We begin with the time-independent Gross-Pitaevskii equation and show how to reformulate it into a singularly perturbed nonlinear eigenvalue problem under a constraint. Matched asymptotic approximations for the problem are reviewed to confirm the asymptotic behaviors of the solutions in the boundary/interior layer regions. By using the normalized gradient flow, we propose an adaptive finite element with hybrid basis to solve the singularly perturbed nonlinear eigenvalue problem. Our basis functions and the mesh are chosen adaptively to the small parameter ε. Extensive numerical results are reported to show the uniform convergence property of our method. We also apply the AFEM-HB to compute the ground and excited states of BEC with box/harmonic/optical lattice potential in the semiclassical regime (0 <ε≪C 1). In addition, we give a detailed error analysis of our AFEM-HB to a simpler singularly perturbed two point boundary value problem, show that our method has a minimum uniform convergence order 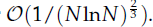
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2016
References
- 2
- Cited by


