Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T12:11:55.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Adaptive Stokes Preconditioning for Steady Incompressible Flows

Part of: Hydrodynamic stability Numerical problems in dynamical systems Approximation methods and numerical treatment of dynamical systems Numerical linear algebra Incompressible viscous fluids Applications - Dynamical systems and ergodic theory Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  21 June 2017

Cédric Beaume
Cédric Beaume*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, United Kingdom
*
*Corresponding author. Email address:[email protected] (C. Beaume)
Get access

Abstract

This paper describes an adaptive preconditioner for numerical continuation of incompressible Navier–Stokes flows based on Stokes preconditioning [42] which has been used successfully in studies of pattern formation in convection. The preconditioner takes the form of the Helmholtz operator I–ΔtL which maps the identity (no preconditioner) for Δt≪1 to Laplacian preconditioning for Δt≫1. It is built on a first order Euler time-discretization scheme and is part of the family of matrix-free methods. The preconditioner is tested on two fluid configurations: three-dimensional doubly diffusive convection and a two-dimensional projection of a shear flow. In the former case, it is found that Stokes preconditioning is more efficient for 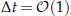, away from the values used in the literature. In the latter case, the simple use of the preconditioner is not sufficient and it is necessary to split the system of equations into two subsystems which are solved simultaneously using two different preconditioners, one of which is parameter dependent. Due to the nature of these applications and the flexibility of the approach described, this preconditioner is expected to help in a wide range of applications.

Keywords

Fluid dynamicshydrodynamic stabilitynumerical continuationpreconditioningStokes preconditioningdoubly diffusive convectionshear flows

MSC classification

Secondary: 35Q30: Navier-Stokes equations 35Q35: PDEs in connection with fluid mechanics 37M20: Computational methods for bifurcation problems 37N10: Dynamical systems in fluid mechanics, oceanography and meteorology 65F08: Preconditioners for iterative methods 65P30: Bifurcation problems 76D05: Navier-Stokes equations 76E05: Parallel shear flows 76E06: Convection
Type
Research Article
Information
Communications in Computational Physics , Volume 22 , Issue 2 , August 2017 , pp. 494 - 516
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barkley, D., Gomes, M. G. M. and Henderson, R. D., Three-dimensional instability in flow over a backward-facing step, J. Fluid Mech., 473 (2002), 167–190.CrossRefGoogle Scholar
[2] Batiste, O., Knobloch, E., Alonso, A. and Mercader, I., Spatially localized binary-fluid convection, J. Fluid Mech., 560 (2006), 149–158.Google Scholar
[3] Beaume, C., Bergeon, A., Kao, H.-C. and Knobloch, E., Convectons in a rotating fluid layer, J. Fluid Mech., 717 (2013), 417–448.CrossRefGoogle Scholar
[4] Beaume, C., Bergeon, A. and Knobloch, E., Homoclinic snaking of localized states in doubly diffusive convection, Phys. Fluids, 23 (2011), 094102.CrossRefGoogle Scholar
[5] Beaume, C., Bergeon, A. and Knobloch, E., Convectons and secondary snaking in three-dimensional natural doubly diffusive convection, Phys. Fluids, 25 (2013), 024105.Google Scholar
[6] Beaume, C., Chini, G. P., Julien, K. and Knobloch, E., Reduced description of exact coherent states in parallel shear flows, Phys. Rev. E, 91 (2015), 043010.CrossRefGoogle ScholarPubMed
[7] Beaume, C., Kao, H.-C., Knobloch, E. and Bergeon, A., Localized rotating convection with no-slip boundary conditions, Phys. Fluids, 25 (2013), 124105.CrossRefGoogle Scholar
[8] Beaume, C., Knobloch, E. and Bergeon, A., Nonsnaking doubly diffusive convectons and the twist instability, Phys. Fluids, 25 (2013), 114102.Google Scholar
[9] Bergeon, A., Henry, D., Ben Hadid, H. and Tuckerman, L. S., Marangoni convection in binary mixtures with Soret effect, J. Fluid Mech., 375 (1998), 143–177.Google Scholar
[10] Bergeon, A. and Knobloch, E., Natural doubly diffusive convection in three-dimensional enclosures, Phys. Fluids, 14 (2002), 3233–3250.Google Scholar
[11] Borońska, K. and Tuckerman, L. S., Extreme multiplicity in cylindrical Rayleigh–Bénard convection II. Bifurcation diagram and symmetry classification, Phys. Rev. E, 81 (2010), 036321.Google Scholar
[12] Chantry, M., Willis, A. P. and Kerswell, R. R., Genesis of streamwise-localized solutions from globally periodic traveling waves in pipe flow, Phys. Rev. Lett., 112 (2014), 164501.Google Scholar
[13] Clever, R. M. and Busse, F. H., Tertiary and quaternary solutions for plane Couette flow, J. Fluid Mech., 344 (1997), 137–153.Google Scholar
[14] Clewley, R.H., Sherwood, W. E., LaMar, M.D. and Guckenheimer, J.M., PyDSTool, A Software Environment for Dynamical Systems Modeling, (2007).Google Scholar
[15] der Vorst, H. A. V., Bi-CGSTAB: A fast and smoothly converging variant of bi-CG for the solution of nonsymmetric linear systems, SIAM J. Sci. Stat. Comput., 13 (1992), 631–644.Google Scholar
[16] Dijkstra, H. A., Wubs, F. W., Cliffe, A. K., Doedel, E., Dragomirescu, I. F., Eckhardt, B., Gelfgat, A. Y., Hazel, A. L., Lucarini, V., Salinger, A. G., Phipps, E. T., Sanchez-Umbria, J., Schuttelaars, H., Tuckerman, L. S. and Thiele, U., Numerical bifurcation methods and their applications to fluid dynamics: analysis beyond simulation, Commun. Comput. Phys., 15 (2014), 1–45.Google Scholar
[17] Doedel, E. J., Champneys, A. R., Dercole, F., Fairgrieve, T., Kuznetsov, Y., Oldeman, B., Paffenroth, R., Sandstede, B., Wang, X. and Zhang, C., AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equations, 2008.Google Scholar
[18] Engelborghs, K., Luzyanina, T. and Samaey, G., DDE-BIFTOOL v. 2.00: a Matlab package for bifurcation analysis of delay differential equations, Technical Report TW-330, Dep. Comp. Sci., KU Leuven, (2001).Google Scholar
[19] Faisst, H. and Eckhardt, B., Traveling waves in pipe flow, Phys. Rev. Lett., 91 (2003), 224502.Google Scholar
[20] Feudel, F., Bergemann, K., Tuckerman, L. S., Egbers, C., Futterer, B., Gellert, M. and Hollerbach, R., Convection patterns in a spherical fluid shell, Phys. Rev. E, 83 (2011), 046304.Google Scholar
[21] Frigo, M. and Johnson, S. G., The design and implementation of FFTW3, Proceedings of the IEEE, 93 (2005), 216–231.CrossRefGoogle Scholar
[22] Gibson, J. F., Channelflow: A spectral Navier–Stokes simulator in C++, tech. rep., U. New Hampshire, 2012. http://channelflow.org/.Google Scholar
[23] Gibson, J. F. and Brand, E., Spanwise-localized solutions of planar shear flows, J. Fluid Mech., 745 (2014), 25–61.Google Scholar
[24] Gibson, J. F., Halcrow, J. and Cvitanović, P., Equilibrium and travelling-wave solutions of plane Couette flow, J. Fluid Mech., 638 (2009), 243–266.Google Scholar
[25] Kawahara, G., Uhlmann, M. and van Veen, L., The significance of simple invariant solutions in turbulent flows, Annu. Rev. Fluid Mech., 44 (2012), 203–225.CrossRefGoogle Scholar
[26] Keller, H. B., Numerical Solutions of Bifurcation and Non-Linear Eigenvalues Problem: Application of Bifurcation Theory, Academic Press New York, (1977).Google Scholar
[27] Krauskopf, B., Osinga, H. M. and Galán-Viosque, J., Numerical Continuation Methods for Dynamical Systems: Path Following and Boundary Value Problems, Springer-Verlag, 2007.Google Scholar
[28] Kuznetsov, Y. A., Dhooge, A. and Govaerts, W., Matcont: a MATLAB package for numerical bifurcation analysis of ODEs, ACM Trans. Math. Softw., 29 (2003), 141–164.Google Scholar
[29] Lo Jacono, D., Bergeon, A. and Knobloch, E., Magnetohydrodynamic Convectons, J. Fluid Mech., 687 (2011), 595–605.Google Scholar
[30] Lo Jacono, D., Bergeon, A. and Knobloch, E., Three-dimensional spatially localized binary-fluid convection in a porous medium, J. Fluid Mech., 730 (2013), R2.Google Scholar
[31] Mamun, C. K. and Tuckerman, L. S., Asymmetry and Hopf bifurcation in spherical Couette flow, Phys. Fluids, 7 (1995), 80–91.Google Scholar
[32] Melnikov, K., Kreilos, T. and Eckhardt, B., Long-wavelength instability of coherent structures in plane Couette flow, Phys. Rev. E, 89 (2014), 043008.Google Scholar
[33] Mercader, I., Batiste, O., Alonso, A. and Knobloch, E., Localized pinning states in closed containers: Homoclinic snaking without bistability, Phys. Rev. E, 80 (2009), 025201(R).CrossRefGoogle ScholarPubMed
[34] Mercader, I., Batiste, O., Alonso, A. and Knobloch, E., Convectons, anticonvectons and multiconvectons in binary fluid convection, J. Fluid Mech., 667 (2011), 586–606.Google Scholar
[35] Nagata, M., Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity, J. Fluid Mech., 217 (1990), 519–527.Google Scholar
[36] Pringle, C. C. T. and Kerswell, R. R., Asymmetric, helical and mirror-symmetric traveling waves in pipe flow, Phys. Rev. Lett., 99 (2007), 074502.Google Scholar
[37] Sanchez, J., Marques, F. and Lopez, J.M., A continuation and bifurcation technique for Navier–Stokes flows, J. Comput. Phys., 180 (2002), 78–98.Google Scholar
[38] Schneider, T. M., Gibson, J. F. and Burke, J., Snakes and ladders: Localized solutions of plane Couette flow, Phys. Rev. Lett., 104 (2010), 104501.Google Scholar
[39] Seydel, R., Practical Bifurcation and Stability Analysis, Interdisciplinary Applied Mathematics, Springer, 2009.Google Scholar
[40] Seydel, R. and Hlavacek, V., Role of continuation in engineering analysis, Chem. Eng. Sci., 42 (1987), 1281–1295.Google Scholar
[41] Torres, J. F., Henry, D., Komiya, A. and Maruyama, S., Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls, J. Fluid Mech., 756 (2014), 650–688.Google Scholar
[42] Tuckerman, L. S., Steady-state solving via stokes preconditioning; recursion relations for elliptic operators, in 11th International Conference on Numerical Methods in Fluid Dynamics, Dwoyer, D., Hussaini, M. and Voigt, R., eds., vol. 323 of Lecture Notes in Physics, Springer Berlin Heidelberg, 1989, 573–577.Google Scholar
[43] Tuckerman, L. S., Laplacian preconditioning for the inverse Arnoldi method, Commun. Comput. Phys., 18 (2015), 1336–1351.Google Scholar
[44] Uecker, H., Wetzel, D. and Rademacher, J. D. M., Pde2path–a Matlab package for continuation and bifurcation in 2D elliptic systems, Numer. Math. Theor. Methods Appl., 7 (2014), 58–106.Google Scholar
[45] Viswanath, D., The critical layer in pipe flow at high Reynolds numbers, Phil. Trans. R. Soc. A, 367 (2009), 561–576.Google Scholar
[46] Waleffe, F., Homotopy of exact coherent structures in plane shear flows, Phys. Fluids, 15 (2003), 1517–1534.Google Scholar
[47] Wang, J., Gibson, J. and Waleffe, F., Lower branch coherent states in shear flows: Transition and control, Phys. Rev. Lett., 98 (2007), 204501.Google Scholar
[48] Wedin, H. and Kerswell, R. R., Exact coherent structures in pipe flow: travelling wave solutions, J. Fluid Mech., 508 (2004), 333–371.CrossRefGoogle Scholar