Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T07:49:53.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted counting of solutions to sparse systems of equations

Part of: Discrete geometry Equilibrium statistical mechanics Polytopes and polyhedra Theory of computing Algorithms - Computer Science

Published online by Cambridge University Press:  15 April 2019

Alexander Barvinok  and
Guus Regts
Alexander Barvinok*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109-1043, USA
Guus Regts
Affiliation:
Korteweg de Vries Institute for Mathematics, University of Amsterdam, P.O. Box 94248, 1090 GE Amsterdam, The Netherlands
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

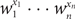Given complex numbers w1,…,wn, we define the weight w(X) of a set X of 0–1 vectors as the sum of $w_1^{x_1} \cdots w_n^{x_n}$ over all vectors (x1,…,xn) in X. We present an algorithm which, for a set X defined by a system of homogeneous linear equations with at most r variables per equation and at most c equations per variable, computes w(X) within relative error ∊ > 0 in (rc)O(lnn-ln∊) time provided 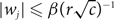$|w_j| \leq \beta (r \sqrt{c})^{-1}$ for an absolute constant β > 0 and all j = 1,…,n. A similar algorithm is constructed for computing the weight of a linear code over 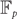${\mathbb F}_p$. Applications include counting weighted perfect matchings in hypergraphs, counting weighted graph homomorphisms, computing weight enumerators of linear codes with sparse code generating matrices, and computing the partition functions of the ferromagnetic Potts model at low temperatures and of the hard-core model at high fugacity on biregular bipartite graphs.

MSC classification

Primary: 68Q25: Analysis of algorithms and problem complexity
Secondary: 68W25: Approximation algorithms 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs 52C07: Lattices and convex bodies in $n$ dimensions 52B55: Computational aspects related to convexity
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 5 , September 2019 , pp. 696 - 719
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research partially supported by NSF grant DMS 1361541.

‡

Research supported by a personal NWO Veni grant.

References

Ausiello, G., Crescenzi, P., Gambosi, G., Kann, V., Marchetti-Spaccamela, A., and Protasi, M. (1999) Complexity and Approximation: Combinatorial Optimization Problems and their Approximability Properties, Springer.CrossRefGoogle Scholar
Barvinok, A. (2016) Combinatorics and Complexity of Partition Functions, Vol. 30 of Algorithms and Combinatorics, Springer.CrossRefGoogle Scholar
Barvinok, A. (2017) Computing the partition function of a polynomial on the Boolean cube. In A Journey Through Discrete Mathematics (Loebl, M., et al., eds), Springer, pp. 135–164.CrossRefGoogle Scholar
Barvinok, A. (2018) Computing permanents of complex diagonally dominant matrices and tensors. Israel J. Math., to appear. arXiv:1801.04191Google Scholar
van den Berg, J. and Steif, J. E. (1994) Percolation and the hard-core lattice gas model. Stoch. Process. Appl. 49 179–197.CrossRefGoogle Scholar
Berlekamp, E. R, McEliece, R. J. and van Tilborg, H. C. A. (1978) On the inherent intractability of certain coding problems. IEEE Trans. Inform. Theory 24 384–386.CrossRefGoogle Scholar
Borgs, C., Chayes, J., Kahn, J., and Lovász, L. (2013) Left and right convergence of graphs with bounded degree. Random Struct. Alg. 42 1–28.CrossRefGoogle Scholar
Bruck, J. and M. Naor, M. (1990) The hardness of decoding linear codes with preprocessing. IEEE Trans. Inform. Theory 36 381–385.CrossRefGoogle Scholar
Bukh, B. (2015) Personal communication.Google Scholar
Cai, J.-Y., Galanis, A., Goldberg, L. A., Guo, H., Jerrum, M., Štefankovič, D. and Vigoda, E. (2016) #BIS-hardness for 2-spin systems on bipartite bounded degree graphs in the tree non-uniqueness region. J. Comput. System Sci. 82 690–711.CrossRefGoogle Scholar
Chen, S., Delcourt, M., Moitra, A., Perarnau, G., and Postle, L. (2019) Improved bounds for randomly sampling colorings via linear programming. In Proc. Thirtieth Annual ACM–SIAM Symposium on Discrete Algorithms, SIAM, pp. 2216–2234.CrossRefGoogle Scholar
Csikvári, P. and Frenkel, P. E. (2016) Benjamini–Schramm continuity of root moments of graph polynomials. Europ. J. Combin. 52 (part B), 302–320.CrossRefGoogle Scholar
Diestel, R. (2005) Graph Theory, third edition, Vol. 173 of Graduate Texts in Mathematics, Springer.Google Scholar
Friedli, S. and Velenik, Y. (2018) Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction, Cambridge University Press.Google Scholar
Helmuth, T., Perkins, W., and Regts, G.(2018) Algorithmic Pirogov–Sinai theory. In Proceedings of the 51st Annual ACM Symposium on the Theory of Computing (STOC 2019).CrossRefGoogle Scholar
Jenssen, M., Keevash, P., and Perkins, W.(2019) Algorithms for #BIS-hard problems on expander graphs. In Proc. Thirtieth Annual ACM–SIAM Symposium on Discrete Algorithms, SIAM, pp. 2235–2247.CrossRefGoogle Scholar
Krantz, S. G. (1992) Function Theory of Several Complex Variables, second edition, Wadsworth & Brooks/Cole Mathematics Series, Wadsworth & Brooks/Cole.Google Scholar
van Lint, J. H. (1999) Introduction to Coding Theory, third edition, Vol. 86 of Graduate Texts in Mathematics, Springer.CrossRefGoogle Scholar
Liu, J., Sinclair, A., and Srivastava, P.(2019) The Ising partition function: Zeros and deterministic approximation. J. Statist. Phys. 174, 287–315.CrossRefGoogle Scholar
Mézard, M. and Montanari, A. (2009) Information, Physics, and Computation, Oxford Graduate Texts, Oxford University Press.CrossRefGoogle Scholar
Patel, V. and Regts, G. (2017) Deterministic polynomial-time approximation algorithms for partition functions and graph polynomials. SIAM J. Comput. 46 1893–1919.CrossRefGoogle Scholar
Patel, V. and Regts, G. (2017) Computing the number of induced copies of a fixed graph in a bounded degree graph. Algorithmica. doi: 10.1007/s00453-018-0511-9CrossRefGoogle Scholar
Valiant, L. G. (1979) The complexity of computing the permanent. Theoret. Comput. Sci. 8 189–201.CrossRefGoogle Scholar
Valiant, L. G. and Vazirani, V. V. (1986) NP is as easy as detecting unique solutions. Theoret. Comput. Sci. 47 85–93.CrossRefGoogle Scholar
Vigoda, E. (2000) Improved bounds for sampling colorings. J. Math. Phys. 41 1555–1569.CrossRefGoogle Scholar