Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T06:03:36.231Z Has data issue: false hasContentIssue false
  • English
  • Français

A Weakening of the Odd Hadwiger's Conjecture

Published online by Cambridge University Press:  01 November 2008

KEN-ICHI KAWARABAYASHI
KEN-ICHI KAWARABAYASHI*
Affiliation:
National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Gerards and Seymour (see [10], p. 115) conjectured that if a graph has no odd complete minor of order l, then it is (l − 1)-colourable. This is an analogue of the well-known conjecture of Hadwiger, and in fact, this would immediately imply Hadwiger's conjecture. The current best-known bound for the chromatic number of graphs with no odd complete minor of order l is 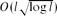by the recent result by Geelen, Gerards, Reed, Seymour and Vetta [8], and by Kawarabayashi [12] later, independently. But it seems very hard to improve this bound since this would also improve the current best-known bound for the chromatic number of graphs with no complete minor of order l.

Motivated by this problem, in this note we show that there exists an absolute constant f(k) such that any graph G with no odd complete minor of order k admits a vertex partition V1, . . ., V496k such that each component in the subgraph induced on Vi (i ≥ 1) has at most f(k) vertices. When f(k) = 1, this is a colouring of G. Hence this is a relaxation of colouring in a sense, and this is the first result in this direction for the odd Hadwiger's conjecture.

Our proof is based on a recent decomposition theorem due to Geelen, Gerards, Reed, Seymour and Vetta [8], together with a connectivity result that forces a huge complete bipartite minor in large graphs by Böhme, Kawarabayashi, Maharry and Mohar [3].

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 6 , November 2008 , pp. 815 - 821
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Appel, K. and Haken, W. (1977) Every planar map is four colorable I: Discharging. Illinois J. Math. 21 429–490.Google Scholar
[2]Appel, K., Haken, W. and Koch, J. (1977) Every planar map is four colorable II: Reducibility. Illinois J. Math. 21 491–567.Google Scholar
[3]Böhme, T., Kawarabayashi, K., Maharry, J. and Mohar, B. Linear connectivity forces large complete bipartite minors. J. Combin. Theory Ser. B (submitted).Google Scholar
[4]Catlin, P. A. (1978) A bound on the chromatic number of a graph. Discrete Math. 22 81–83.CrossRefGoogle Scholar
[5]Diestel, R. (2000) Graph Theory, 2nd edn, Springer.Google Scholar
[6]Dirac, G. A. (1952) A property of 4-chromatic graphs and some remarks on critical graphs. J. London Math. Soc. 27 85–92.CrossRefGoogle Scholar
[7]Hadwiger, H. (1943) Über eine Klassifikation der Streckenkomplexe. Vierteljahrsschr. naturforsch. Ges. Zürich 88 133–142.Google Scholar
[8]Geelen, J., Gerards, B., Reed, B., Seymour, P. and Vetta, A. On the odd-minor variant of Hadwiger's conjecture. J. Combin. Theory Ser. B (submitted).Google Scholar
[9]Guenin, B. Talk at Oberwolfach on graph theory, January 2005.Google Scholar
[10]Jensen, T. R. and Toft, B. (1995) Graph Coloring Problems, Wiley–Interscience.Google Scholar
[11]Kawarabayashi, K. Minors in 7-chromatic graphs. Preprint.Google Scholar
[12]Kawarabayashi, K. Note on coloring graphs without odd K k-minors. J. Combin. Theory Ser. B (submitted).Google Scholar
[13]Kawarabayashi, K. and Mohar, B. (2007) A relaxed Hadwiger's conjecture for list-colorings. J. Combin. Theory Ser. B 97 647–651.CrossRefGoogle Scholar
[14]Kawarabayashi, K. and Song, Z. (2007) Some remarks on the odd Hadwiger's conjecture. Combinatorica 27 429–438.CrossRefGoogle Scholar
[15]Kawarabayashi, K. and Toft, B. (2005) Any 7-chromatic graph has K 7 or K 4,4 as a minor. Combinatorica 25 327–353.CrossRefGoogle Scholar
[16]Kostochka, A. (1982) The minimum Hadwiger number for graphs with a given mean degree of vertices. Metody Diskret. Analiz. 38 37–58. (In Russian.)Google Scholar
[17]Kostochka, A. (1984) Lower bound of the Hadwiger number of graphs by their average degree. Combinatorica 4 307–316.CrossRefGoogle Scholar
[18]Robertson, N., Seymour, P. D. and Thomas, R. (1993) Hadwiger's conjecture for K 6-free graphs. Combinatorica 13 279–361.CrossRefGoogle Scholar
[19]Robertson, N., Sanders, D. P., Seymour, P. D. and Thomas, R. (1997) The four-color theorem. J. Combin. Theory Ser. B 70 2–44.CrossRefGoogle Scholar
[20]Thomason, A. (1984) An extremal function for contractions of graphs. Math. Proc. Cambridge Philos. Soc. 95 261–265.CrossRefGoogle Scholar
[21]Thomason, A. (2001) The extremal function for complete minors. J. Combin. Theory Ser. B 81 318–338.CrossRefGoogle Scholar
[22]Wagner, K. (1937) Über eine Eigenschaft der ebenen Komplexe. Math. Ann. 114 570–590.CrossRefGoogle Scholar