Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T16:48:39.408Z Has data issue: false hasContentIssue false
  • English
  • Français

WDM and Directed Star Arboricity

Published online by Cambridge University Press:  05 February 2010

OMID AMINI ,
FRÉDÉRIC HAVET ,
FLORIAN HUC  and
STÉPHAN THOMASSÉ
OMID AMINI
Affiliation:
Projet Mascotte, CNRS/INRIA/UNSA, INRIA Sophia-Antipolis, 2004 route des Lucioles BP 93, 06902 Sophia-Antipolis Cedex, France (e-mail: [email protected], [email protected], [email protected])
FRÉDÉRIC HAVET
Affiliation:
Projet Mascotte, CNRS/INRIA/UNSA, INRIA Sophia-Antipolis, 2004 route des Lucioles BP 93, 06902 Sophia-Antipolis Cedex, France (e-mail: [email protected], [email protected], [email protected])
FLORIAN HUC
Affiliation:
Projet Mascotte, CNRS/INRIA/UNSA, INRIA Sophia-Antipolis, 2004 route des Lucioles BP 93, 06902 Sophia-Antipolis Cedex, France (e-mail: [email protected], [email protected], [email protected])
STÉPHAN THOMASSÉ
Affiliation:
LIRMM, 161 rue ADA, Montpellier, France (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A digraph is m-labelled if every arc is labelled by an integer in {1, . . ., m}. Motivated by wavelength assignment for multicasts in optical networks, we introduce and study n-fibre colourings of labelled digraphs. These are colourings of the arcs of D such that at each vertex v, and for each colour α, in(v, α) + out(v, α) ≤ n with in(v, α) the number of arcs coloured α entering v and out(v, α) the number of labels l such that there is at least one arc of label l leaving v and coloured with α. The problem is to find the minimum number of colours λn(D) such that the m-labelled digraph D has an n-fibre colouring. In the particular case when D is 1-labelled, λ1(D) is called the directed star arboricity of D, and is denoted by dst(D). We first show that dst(D) ≤ 2Δ−(D)+1, and conjecture that if Δ−(D) ≥ 2, then dst(D) ≤ 2Δ−(D). We also prove that for a subcubic digraph D, then dst(D) ≤ 3, and that if Δ+(D), Δ−(D) ≤ 2, then dst(D) ≤ 4. Finally, we study λn(m, k) = max{λn(D) | D is m-labelled and Δ−(D) ≤ k}. We show that if m ≥ n, then 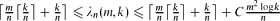for some constant C. We conjecture that the lower bound should be the correct value of λn(m, k).

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 2 , March 2010 , pp. 161 - 182
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Algor, I. and Alon, N. (1989) The star arboricity of graphs. Discrete Math. 75 11–22.CrossRefGoogle Scholar
[2]Alon, N., McDiarmid, C. and Reed, B. (1992) Star arboricity. Combinatorica 12 375–380.CrossRefGoogle Scholar
[3]Brandt, R. (2003) Multicasting using WDM in multifiber optical star networks. Thesis, UCSB.Google Scholar
[4]Brandt, R. and Gonzalez, T. F. (2005) Wavelength assignment in multifiber optical star networks under the multicasting communication mode. J. Interconnection Networks 6 383–405.CrossRefGoogle Scholar
[5]Frank, A. (1979) Covering branchings. Acta Scientiarum Mathematicarum (Szeged) 41 77–81.Google Scholar
[6]Guiduli, B. (1997) On incidence coloring and star arboricity of graphs. Discrete Math. 163 275–278.CrossRefGoogle Scholar
[7]Lardies, A., Gupta, R. and Patterson, R. (2001) Traffic grooming in a multi-layer network. Optical Networks Magazine 2 91–99.Google Scholar
[8]Modiano, E. and Lin, P. J. (2001) Traffic grooming in WDM networks. IEEE Communications Magazine 39 124–129.CrossRefGoogle Scholar
[9]Pinlou, A. and Sopena, E. (2006) The acircuitic directed star arboricity of subcubic graph is at most four. Discrete Math. 306 3281–3289.CrossRefGoogle Scholar
[10]Schrijver, A. (2003) Combinatorial Optimization: Polyhedra and Efficiency, Vol. 24 of Algorithms and Combinatorics, Springer, Berlin.Google Scholar
[11]Vizing, V. G. (1964) On an estimate of the chromatic class of a p-graph. Metody Diskret. Analyz. 3 25–30.Google Scholar